Solutions détaillées de neuf exercices sur la notion d’opération sur un ensemble (fiche 01).
Cliquer ici pour accéder aux énoncés

On calcule d’une part :
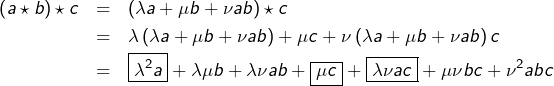
et d’autre part :
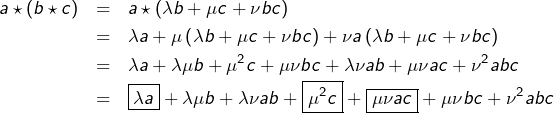
Les termes non encadrés se retrouvent dans les deux expressions. Pour que celles-ci soient égales pour tout triplet
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{cccc}\lambda^{2} & = & \lambda & (1)\\\mu^{2} & = & \mu & (2)\\\lambda\nu & = & \mu\nu & (3)\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f257759094e46d335fa90a94c5c1efbd_l3.png)
Comme le montre l’équation (3), deux cas se présentent :
- si
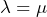 alors
alors 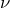 est indéterminé. D’après (1) et (2) :
est indéterminé. D’après (1) et (2) : 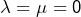 ou
ou 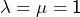
- si
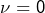 alors
alors 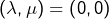 ou
ou 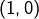 ou
ou 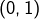 ou
ou 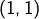
Ainsi, les opérations de cette forme qui sont associatives sont données par :
![]()
![]()
![]()
![]()
Soit ![]()
Supposons l’existence d’une matrice ![]() telle que
telle que ![]() En passant aux déterminants, on voit que :
En passant aux déterminants, on voit que : ![]()
Comme ![]() et
et ![]() sont des entiers, ceci impose notamment
sont des entiers, ceci impose notamment ![]()
Réciproquement, notons ![]() et supposons que
et supposons que ![]() En posant
En posant ![]() (qui est, comme
(qui est, comme ![]() , élément de
, élément de ![]() ), on observe que :
), on observe que :
![]()
Par anti-commutativité du produit vectoriel, la condition ![]() équivaut à :
équivaut à :
![]()
![]()
![]()
Cette égalité est vérifiée dès que la famille ![]() est liée.
est liée.
Et si ![]() est libre, alors
est libre, alors ![]()
Bref, la condition cherchée est :
![]()

Supposons que ![]() est inversible à gauche. Il existe donc
est inversible à gauche. Il existe donc ![]() vérifiant
vérifiant ![]() Comme
Comme ![]() est injective, ceci impose à
est injective, ceci impose à ![]() d’être injective.
d’être injective.
Réciproquement, si ![]() est injective, on peut définir une application
est injective, on peut définir une application ![]() en associant à chaque élément de
en associant à chaque élément de ![]() son unique antécédent par
son unique antécédent par ![]() et en associant à chaque élément de
et en associant à chaque élément de ![]() un élément quelconque, préalablement choisi dans
un élément quelconque, préalablement choisi dans ![]()
Il est alors clair que ![]() ce qui prouve que :
ce qui prouve que :
![]()
Si ![]() est inversible à droite, alors c’est qu’il existe
est inversible à droite, alors c’est qu’il existe ![]() telle que
telle que ![]() ce qui entraîne la surjectivité de
ce qui entraîne la surjectivité de ![]() (puisque
(puisque ![]() est surjective).
est surjective).
Réciproquement, supposons ![]() surjective. L’axiome du choix permet d’associer à chaque élément de
surjective. L’axiome du choix permet d’associer à chaque élément de ![]() un élément choisi dans
un élément choisi dans ![]() (qui est non vide par hypothèse). On dispose ainsi d’une application
(qui est non vide par hypothèse). On dispose ainsi d’une application ![]() vérifiant
vérifiant ![]() Par conséquent :
Par conséquent :
![]()

Soient ![]() et
et ![]() deux suites réelles.
deux suites réelles.
Par définition :
![]()
![Rendered by QuickLaTeX.com \[u_{n}=\sum_{k=0}^{n}a_{k}b_{n-k}\underset{\diamondsuit}{=}\sum_{j=0}^{n}a_{n-j}b_{j}=v_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3c6136667cf0acc16447f6a15575f9ae_l3.png)
Passons à l’associativité. Ajoutons une troisième suite réelle ![]() Par définition :
Par définition :
![]()
![Rendered by QuickLaTeX.com \[ x{n}=\sum_{k=0}^{n}\left(\sum_{j=0}^{k}a_{j}b_{k-j}c_{n-k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9492f581c05172e7dc9ec47a16ef1a98_l3.png)
![Rendered by QuickLaTeX.com \[y_{n}=\sum_{k=0}^{n}\left(\sum_{j=0}^{n-k}a_{k}b_{j}c_{n-k-j}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c7ab0e22ce3506f9f499aead43d23926_l3.png)
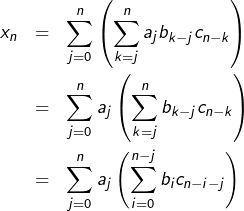
Notons ![]() (
(![]() est le symbole de Kronecker).
est le symbole de Kronecker).
En clair, ![]() est la suite dont les termes successifs sont 1, 0, 0, … etc …
est la suite dont les termes successifs sont 1, 0, 0, … etc …
Pour toute suite réelle ![]() on constate que :
on constate que :
![Rendered by QuickLaTeX.com \[a\star e=\left(c_{n}\right)_{n\in\mathbb{N}}\quad\text{avec }\forall n\in\mathbb{N},\thinspace c_{n}=\sum_{k=0}^{n}a_{k}\delta_{n,k}=a_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-56bf872ca2e5d3fea1941f8fd97904fa_l3.png)
Pour finir, supposons qu’une suite ![]() soit inversible. Il existe donc
soit inversible. Il existe donc ![]() telle que
telle que ![]() En particulier :
En particulier : ![]() ce qui entraîne
ce qui entraîne ![]()
Réciproquement, supposons ![]() et montrons qu’il existe une suite
et montrons qu’il existe une suite ![]() vérifiant
vérifiant ![]() Cette égalité équivaut à :
Cette égalité équivaut à :
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{cccc} & a_{0}b_{0}=1 & & \left(\mathcal{R}_{0}\right)\\\forall n\in\mathbb{N}^{\star}, & {\displaystyle \sum_{k=0}^{n}a_{k}b_{n-k}=0} & & \left(\mathcal{R}_{n}\right)\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d305ca382154f5e78d54e5066faed81a_l3.png)
![Rendered by QuickLaTeX.com \[b_{q+1}=-\frac{1}{a_{0}}\sum_{k=1}^{q+1}a_{k}b_{q+1-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0bfa9b3ca511fb97034fd3b710591063_l3.png)
Remarque
Ces calculs constituent les premiers pas de la construction de l’algèbre ![]() des séries formelles à une indéterminée sur le corps des réels.
des séries formelles à une indéterminée sur le corps des réels.
Pour l’équation ![]() il n’existe aucune solution si
il n’existe aucune solution si ![]()
Supposons maintenant que ![]() Pour tout
Pour tout ![]() on peut écrire :
on peut écrire : ![]() (où
(où ![]() désigne le complémentaire de
désigne le complémentaire de ![]() dans
dans ![]()
Donc si ![]() est solution, alors il existe
est solution, alors il existe ![]() tel que
tel que ![]()
Réciproquement, si ![]() est de cette forme, alors
est de cette forme, alors ![]() , puisque
, puisque ![]() et
et ![]()
En conclusion, l’ensemble de solutions de ![]() est :
est :
![Rendered by QuickLaTeX.com \[\boxed{\mathcal{S}=\left\{ \begin{array}{cc}\emptyset & \text{si }B\not\subset A\\\\\left\{ B\cup Y;\thinspace Y\in\mathcal{P}\left(\overline{A}\right)\right\} & \text{sinon}\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-53772a7866425aa8473b492afdb4b708_l3.png)
Pour l’équation ![]() il n’existe aucune solution si
il n’existe aucune solution si ![]()
Supposons désormais que ![]() Si
Si ![]() vérifie
vérifie ![]() alors
alors ![]() donc (faire un dessin peut aider) :
donc (faire un dessin peut aider) :
![]()
![]()
Réciproquement, si ![]() est de cette forme, alors
est de cette forme, alors ![]()
Finalement, l’ensemble de solutions de ![]() est :
est :
![Rendered by QuickLaTeX.com \[\boxed{\mathcal{S}=\left\{ \begin{array}{cc}\emptyset & \text{si }A\not\subset B\\\\\left\{ \left(B-A\right)\cup Y;\thinspace Y\in\mathcal{P}\left(A\right)\right\} & \text{sinon}\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e53b9b6abf4d3ba4645fbf5318fb98cf_l3.png)
Munissons ![]() du produit matriciel.
du produit matriciel.
On sait bien que, pour cette opération, il existe un élément neutre à savoir ![]()
Considérons l’ensemble ![]() .
.
![]() est une partie de
est une partie de ![]() stable pour le produit matriciel, mais il n’existe pas de matrice
stable pour le produit matriciel, mais il n’existe pas de matrice ![]() telle que
telle que ![]()
En effet, il existe dans ![]() des matrices inversibles, comme par exemple
des matrices inversibles, comme par exemple ![]() et s’il existait une telle matrice
et s’il existait une telle matrice ![]() l’égalité
l’égalité ![]() impliquerait (en multipliant à droite par
impliquerait (en multipliant à droite par ![]() que
que ![]() ce qui est absurde, vu que
ce qui est absurde, vu que ![]()
Maintenant, considérons l’ensemble :
![]()

Soit ![]() Notons
Notons ![]() un inverse à droite de
un inverse à droite de ![]() et
et ![]() un inverse à droite de
un inverse à droite de ![]() Alors :
Alors :
![]()
![]()
![]()
Ainsi, ![]() est un élément neutre à gauche et donc un élément neutre tout court (et donc l‘élément neutre).
est un élément neutre à gauche et donc un élément neutre tout court (et donc l‘élément neutre).
En outre :
![]()
![]()
![]()
Conclusion : ![]() est un groupe.
est un groupe.
Remarque
Ce résultat est connu sous le nom « d’axiomes faibles » de groupe.

Tout d’abord, l’hypothèse d’associativité donne un sens à ![]() pour tout
pour tout ![]()
Fixons ![]() Comme
Comme ![]() est fini, l’application
est fini, l’application ![]() n’est pas injective.
n’est pas injective.
Il existe donc ![]() tel que
tel que ![]()
Il en résulte, par récurrence, que : ![]()
Pour ![]() il vient
il vient ![]() c’est-à-dire
c’est-à-dire ![]() où l’on a posé
où l’on a posé ![]()
➡ Si ![]() alors
alors ![]() et c’est fini.
et c’est fini.
➡ Si ![]() on multiplie les deux membres de l’égalité
on multiplie les deux membres de l’égalité ![]() par
par ![]() ce qui donne
ce qui donne ![]() soit
soit ![]() avec
avec ![]()
Retenons que dans tout magma associatif fini, il existe au moins un élément idempotent.
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
