Solutions - Exercices sur l’indépendance linéaire

Solutions détaillées de neuf exercices sur l’indépendance linéaire (fiche 01).
Cliquer ici pour accéder aux énoncés.

Le plus simple consiste sans doute à remarquer que :

$\begin{eqnarray*}f\left(x\right) & \underset{{\scriptstyle 0}}{\sim} & x^{2}\\g\left(x\right) & \underset{{\scriptstyle 0}}{\sim} & 2x^{3}\\h\left(x\right) & \underset{{\scriptstyle 0}}{\sim} & 3x^{4}\end{eqnarray*}$

Soient $a,b,c$ des réels tels que, pour tout $x\in\mathbb{R}$ :

$a\thinspace x\sin\left(x\right)+b\thinspace x^{2}\sin\left(2x\right)+c\thinspace x^{3}\sin\left(3x\right)=0$

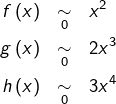
En divisant par $x^{2}$ (pour $x\neq0),$ puis en faisant tendre $x$ vers $0,$ on obtient $a=0.$

On a donc, pour tout $x\neq0$ :

$b\thinspace x^{2}\sin\left(2x\right)+c\thinspace x^{3}\sin\left(3x\right)=0$

En divisant par $x^{3},$ puis en faisant tendre $x$ vers $0,$ on obtient $2b=0,$ donc $b=0.$

Il est alors clair que $c=0.$

Moralité : la famille $\left(f,g,h\right)$ est libre.

On sait que :

$\forall\left(a,b\right)\in\mathbb{R}^{2},\thinspace\sin\left(a+b\right)=\sin\left(a\right)\cos\left(b\right)+\cos\left(a\right)\sin\left(b\right)$

Donc, pour tout $\left(x,y\right)\in\mathbb{R}^{2}$ :

$\begin{eqnarray*}\sin\left(2x+3y\right) & = & \sin\left(\left(x+2y\right)+\left(x+y\right)\right)\\& = & \sin\left(x+2y\right)\cos\left(x+y\right)+\cos\left(x+2y\right)\sin\left(x+y\right) \end{eqnarray*}$

Autrement dit : $F=G+H$ et la famille $\left(F,G,H\right)$ est donc liée.

Toujours grâce à la formule d’addition du sinus (cf. exercice précédent), on observe que chacune des applications $f,g$ et $h$ est combinaison linéaire de $\sin$ et $\cos.$

Autrement dit, $\left(f,g,h\right)$ est une famille de trois vecteurs d’un espace vectoriel de dimension $2$ (le plan engendré par $\sin$ et $\cos).$ Ceci entraîne que $\left(f,g,h\right)$ est liée : on sait en effet que dans un espace vectoriel de dimension $d,$ toute famille comportant plus de $d$ vecteurs est liée.

On peut aussi (mais c’est plus « savant ») invoquer le résultat général qui fait l’objet de l’exercice 8 de cette fiche.

La première affirmation est vraie car « toute sous-famille d’une famille libre est libre ».

La seconde affirmation est fausse. Un exemple : dans $\mathbb{R}^{2},$ si l’on pose $u=\left(1,0\right),$ $v=\left(0,1\right)$ et $w=\left(1,1\right),$ alors chacune des familles $\left(u,v\right),$ $\left(u,w\right)$ et $\left(v,w\right)$ est libre mais la famille $\left(u,v,w\right)$ est liée (puisque $w=u+v$ ou, si l’on préfère, parce que trois vecteurs d’un espace vectoriel de dimension 2 forment nécessairement une famille liée, ou encore et plus fondamentalement en raison du résultat de l’exercice 8 de cette fiche).

La troisième affirmation est fausse. Il se peut en effet que $u=0_{E}$ et que $\left(v,w\right)$ soit libre.

Comme $\left(x_{1},\cdots,x_{n},y\right)$ est liée, il existe des scalaires $\lambda_{1},\cdots,\lambda_{n},\mu$ non tous nuls tels que :

$\lambda_{1}x_{1}+\cdots+\lambda_{n}x_{n}+\mu y=0_{E}$

Si $\mu=0,$ alors l’un au moins des $\lambda_{i}$ est non nul et $\lambda_{1}x_{1}+\cdots+\lambda_{n}x_{n}=0_{E},$ ce qui montre que $\left(x_{1},\cdots,x_{n}\right)$ est liée : contradiction !

Donc $\mu\neq0$ et donc :

$y=-\frac{1}{\mu}\left(\lambda_{1}x_{1}+\cdots+\lambda_{n}x_{n}\right)$

Ainsi $y\in\text{vect}\left\{ x_{1},\cdots,x_{n}\right\}.$

Montrons que si $u$ est injective, alors toute famille libre de vecteurs de $E$ est transformée par $u$ en une famille libre de vecteurs de $F.$

Soit donc $\left(x_{1},\cdots,x_{n}\right)$ une famille libre de vecteurs de $E$ et soient $\lambda_{1},\cdots,\lambda_{n}\in\mathbb{K}$ tels que $\lambda_{1}\thinspace u\left(x_{1}\right)+\cdots+\lambda_{n}\thinspace u\left(x_{n}\right)=0_{F}.$

Comme $u$ est linéaire, cette condition montre que $\lambda_{1}x_{1}+\cdots+\lambda_{n}x_{n}\in\ker\left(u\right),$ c’est-à-dire $\lambda_{1}x_{1}+\cdots+\lambda_{n}x_{n}=0_{E}$ puisque $u$ est injective.

Mais comme $\left(x_{1},\cdots,x_{n}\right)$ est libre, on en déduit la nullité de $\lambda_{i}$ pour tout $i.$ La famille $\left(u\left(x_{1}\right),\cdots,u\left(x_{n}\right)\right)$ est donc libre.

Montrons que si $u$ est surjective, alors toute famille génératrice de $E$ est transformée par $u$ en une famille génératrice de $F.$

Soit $y\in F.$ Comme $u$ est surjective, il existe $x\in E$ tel que $y=u\left(x\right).$ Puis, comme $\left(x_{1},\cdots,x_{n}\right)$ est une famille génératrice de $E,$ il existe $\lambda_{1},\cdots,\lambda_{n}\in\mathbb{K}$ tels que $x=\lambda_{1}x_{1}+\cdots+\lambda_{n}x_{n}.$

Par linéarité de $u,$ on en déduit que $y=\lambda_{1}\thinspace u\left(x_{1}\right)+\cdots+\lambda_{n}\thinspace u\left(x_{n}\right).$ On a bien montré que tout vecteur de $F$ est combinaison linéaire de $u\left(x_{1}\right),\cdots,u\left(x_{n}\right).$

On va utiliser que le fait que, pour tout polynôme $Q\left(X\right)\in\mathbb{R}\left[X\right]$ de degré $n$ et pour tout $a\in\mathbb{R}$ :

$Q\left(X+a\right)=\sum_{k=0}^{n}\frac{a^{k}}{k!}Q\left(X\right)^{\left(k\right)}$

Soient $\lambda_{0},\cdots,\lambda_{n}\in\mathbb{R}$ tels que :

$\sum_{j=0}^{n}\lambda_{j}\thinspace P\left(X+t_{j}\right)=0$

Cette condition peut donc s’écrire aussi :

$\sum_{j=0}^{n}\left[\lambda_{j}\sum_{k=0}^{n}\frac{t_{j}^{k}}{k!}P\left(X\right)^{k}\right]=0$

soit, après interversion des deux sommes (voir si nécessaire cet article) :

$\sum_{k=0}^{n}\left[\sum_{j=0}^{n}\lambda_{j}\thinspace\frac{t_{j}^{k}}{k!}\right]\frac{P\left(X\right)^{\left(k\right)}}{k!}=0$

La famille 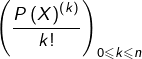$\left(\frac{P\left(X\right)^{\left(k\right)}}{k!}\right)_{0\leqslant k\leqslant n}$ étant libre (polynômes de degrés tous distincts), il s’ensuit que :

$\forall k\in\left\{ 0,\cdots,n\right\} ,\thinspace\sum_{j=0}^{n}\lambda_{j}\thinspace t_{j}^{k}=0$

Il s’agit d’un système linéaire et homogène en les $\lambda_{j},$ qui est de Cramer car son déterminant est le déterminant de Vandermonde :

$\left|\begin{array}{ccccc} 1 & 1 & \cdots & 1 & 1\\ t_{0} & t_{1} & \cdots & t_{n-1} & t_{n}\\ t_{0}^{2} & t_{1}^{2} & \cdots & t_{n-1}^{2} & t_{n}^{2}\\ \vdots & \vdots & & & \vdots\\ t_{0}^{n} & t_{1}^{n} & \cdots & t_{n-1}^{n} & t_{n}^{n} \end{array}\right|=\prod_{0\leqslant i<j\leqslant n}\left(t_{j}-t_{i}\right)\neq0$

Par conséquent : $\lambda_{j}=0$ pour tout $j\in\left\{0,\cdots,n\right\} .$

On a prouvé que la famille $\left(P\left(X+t_{0}\right),\cdots,P\left(X+t_{n}\right)\right)$ est libre.

Preuve de $\boxed{\left(1\right)\Rightarrow\left(2\right)}$

Il s’agit de montrer la surjectivité de l’application

$\theta:E\rightarrow\mathbb{K}^{n},\thinspace v\mapsto\left(\varphi_{1}\left(v\right),\cdots,\varphi_{n}\left(v\right)\right)$

On va procéder indirectement et montrer plutôt son injectivité. Comme $\dim\left(E\right)=n=\dim\left(\mathbb{K}^{n}\right),$ la conclusion résultera du théorème du rang.

Soit donc $v\in\ker\left(\theta\right).$ Pour tout $i\in\left\{1,\cdots,n\right\} ,$ $\varphi_{i}\left(v\right)=0$ et donc, vu que $\left(\varphi_{1},\cdots,\varphi_{n}\right)$ est une base de $\mathcal{L}\left(E,\mathbb{K}\right)$ (famille libre de $n$ vecteurs dans un espace vectoriel de dimension $n),$ il s’ensuit que :

( $\blacktriangle$ ) $\forall\psi\in\mathcal{L}\left(E,\mathbb{K}\right),\:\psi\left(v\right)=0$

Ceci entraîne que $v=0_{E}$ (en effet, dans le cas contraire, on pourrait définir une forme linéaire prenant la valeur $1$ en $x;$ il suffit pour cela de considérer la famille libre réduite au seul vecteur $v,$ de la compléter en une base $\left(v,e_{2},\cdots,e_{n}\right)$ de $E$ puis de définir $\psi\in\mathcal{L}\left(E,\mathbb{K}\right)$ par les images des vecteurs de cette base : $\psi\left(v\right)=1$ et $\psi\left(e_{i}\right)=0$ pour tout $i\in\left\{2,\cdots,n\right\}$ ).

Autre point de vue : on considère une base $(e_1,\ldots,e_n)$ et les formes coordonnées associées $e_i^\star$ pour $1\leqslant i\leqslant n$ . La condition $(\blacktriangle)$ entraîne que $\forall i\in\llbracket1,n\rrbracket,\,e_i^\star(x)=0$ c’est-à-dire $x=0_E$ .

Bref, $\ker\left(\theta\right)=\left\{0_{E}\right\}$ et donc $\theta$ est injective.

Preuve de $\boxed{\left(2\right)\Rightarrow\left(1\right)}$

Il s’agit de montrer que $\left(\varphi_{1},\cdots,\varphi_{n}\right)$ est libre. Soient donc $\lambda_{1},\cdots,\lambda_{n}\in\mathbb{R}$ tels que :

$\sum_{i=1}^{n}\lambda_{i}\varphi_{i}=0\qquad\left(\spadesuit\right)$

Attention : le zéro figurant au second membre désigne bien sûr la forme linéaire nulle.

Pour tout $j\in\left\{1,\cdots,n,\right\}$ on peut associer par hypothèse au $n-$ uplet $\left(\delta_{i,j}\right)_{1\leqslant i\leqslant n},$ un vecteur $v_{j}\in E$ tel que :

$\forall i\in\left\{1,\cdots,n\right\} ,\thinspace\varphi_{i}\left(v_{j}\right)=\delta_{i,j}$

En évaluant le membre de gauche de $\left(\spadesuit\right)$ en $v_{j},$ on obtient $\lambda_{j}=0.$

Remarque : On a utilisé le symbole de Kronecker défini par :

$\delta_{i,j}=\left\{ \begin{array}{cc} 1 & \text{si }i=j\\ \\ 0 & \text{sinon} \end{array}\right.$

Par hypothèse, il existe pour tout $n\in\mathbb{N}$ un couple $\left(\lambda_{n},\mu_{n}\right)\neq\left(0,0\right)$ tel que $\lambda_{n}\,x_{n}+\mu_{n}\,y_{n}=0_{E}.$ Posons :

$\alpha_{n}=\frac{\lambda_{n}}{\sqrt{\lambda_{n}^{2}+\mu_{n}^{2}}}\qquad\text{et}\qquad\beta_{n}=\frac{\mu_{n}}{\sqrt{\lambda_{n}^{2}+\mu_{n}^{2}}}$

Alors :

$\forall n\in\mathbb{N},\,\alpha_{n}\,x_{n}+\beta_{n}\,y_{n}=0_{E}$

et :

$\forall n\in\mathbb{N},\thinspace\alpha_{n}^{2}+\beta_{n}^{2}=1$

d’où en particulier :

$\forall n\in\mathbb{N},\thinspace\left|\alpha_{n}\right|\leqslant1\text{ et }\left|\beta_{n}\right|\leqslant1$

La suite $\alpha$ étant bornée, on peut d’après le théorème de Bolzano-Weierstrass en extraire une sous-suite convergente $\left(\alpha_{\varphi\left(n\right)}\right)_{n\in\mathbb{N}}.$

De même, la suite $\beta$ est bornée, donc la suite $\left(\beta_{\varphi\left(n\right)}\right)$ aussi et l’on peut en extraire une sous-suite convergente $\left(\beta_{\varphi\circ\psi\left(n\right)}\right)_{n\in\mathbb{N}}.$

En posant $\theta=\varphi\circ\psi,$ on constate que les suites $\left(\alpha_{\theta\left(n\right)}\right)$ et $\left(\beta_{\theta\left(n\right)}\right)$ convergent l’une et l’autre, vers des limites respectives $r$ et $s,$ vérifiant :

$r^{2}+s^{2}=\lim_{n\rightarrow\infty}\,\left(\alpha_{\theta\left(n\right)}^{2}+\beta_{\theta\left(n\right)}^{2}\right)=1$

Nécessairement, $\left(r,s\right)\neq\left(0,0\right).$ Et comme $ra+sb=0_{E},$ ceci montre que $\left(a,b\right)$ est liée.

Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.

Partager cet article

Laisser un commentaire Annuler la réponse