Solutions détaillées de neuf exercices sur les éléments propres (fiche 01).
Cliquer ici pour accéder aux énoncés.

Afin de déterminer les valeurs propres de ![]() on peut calculer son polynôme caractéristique :
on peut calculer son polynôme caractéristique :
![]()
On pouvait aussi observer que la trace et le déterminant de ![]() valent respectivement
valent respectivement ![]() et
et ![]() : si l’on note
: si l’on note ![]() les valeurs propres (a priori complexes et éventuellement confondues) de
les valeurs propres (a priori complexes et éventuellement confondues) de ![]() on en déduit que
on en déduit que
![]()
Bref, ![]() possède 2 valeurs propres réelles distinctes, donc est diagonalisable dans
possède 2 valeurs propres réelles distinctes, donc est diagonalisable dans ![]()
Rappel
Une condition suffisante pour qu’un endomorphisme d’un espace vectoriel de dimension ![]() soit diagonalisable est qu’il possède
soit diagonalisable est qu’il possède ![]() valeurs propres distinctes.
valeurs propres distinctes.
Comparer avec cette CNS
Trouvons des vecteurs propres. Le système :
![]()
![]()
![]()
La matrice de passage de la base canonique à la base ![]() est :
est :
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{A^{k}=\left[\begin{array}{cc}2^{k+1}-3^{k} & 2^{k+1}-2\times3^{k}\\3^{k}-2^{k} & 2\times3^{k}-2^{k}\end{array}\right]}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-90dc4ede76fe68b9a8eb64cee6e1dd6b_l3.png)
![]()

Le polynôme caractéristique de ![]() est :
est :
![Rendered by QuickLaTeX.com \[\chi_{A}=\left|\begin{array}{ccc}X-2 & 1 & -1\\1 & X-1 & -2\\-3 & 2 & X-1\end{array}\right|=\left(X-1\right)^{2}\left(X-2\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4ab59e431b2cb641d2b54d1ef1b6bbc7_l3.png)
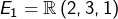 pour la valeur propre 1,
pour la valeur propre 1,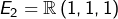 pour la valeur propre 2.
pour la valeur propre 2.
Comme 1 est une valeur propre double et vu que ![]() on voit que
on voit que ![]() n’est pas diagonalisable.
n’est pas diagonalisable.
Rappel
Une condition nécessaire et suffisante pour qu’un endomorphisme d’un ![]() -espace vectoriel de dimension
-espace vectoriel de dimension ![]() soit diagonalisable est que son polynôme caractéristique soit scindé dans
soit diagonalisable est que son polynôme caractéristique soit scindé dans ![]() et que, pour chaque valeur propre, la multiplicité de celle-ci dans le polynôme caractéristique soit égale à la dimension du sev propre correspondant.
et que, pour chaque valeur propre, la multiplicité de celle-ci dans le polynôme caractéristique soit égale à la dimension du sev propre correspondant.
Comparer avec cette autre CNS
Afin de calculer les puissances de ![]() on effectue la division euclidienne de
on effectue la division euclidienne de ![]() par
par ![]() :
:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[A^{2}=\left[\begin{array}{ccc}8 & -5 & 1\\3 & -2 & 3\\11 & -7 & 0\end{array}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8685e59e045a033ad55c9c755bc2ef2e_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{A^{n}=\left[\begin{array}{ccc}5.2^{n}-4n-4 & -3.2^{n}+2n+3 & -2^{n}+2n+1\\5.2^{n}-6n-5 & -3.2^{n}+3n+4 & -2^{n}+3n+1\\5.2^{n}-2n-5 & -3.2^{n}+n+3 & -2^{n}+n+2\end{array}\right]}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1d01b57c1113318ec79022c0c7295439_l3.png)
Il est clair que ![]() est un endomorphisme de
est un endomorphisme de ![]()
On peut observer que pour tout polynôme ![]() :
:
![]()
L’avantage de cette méthode est sa rapidité et l’absence de calcul. Son inconvénient est qu’elle ne fournit pas de base de vecteurs propres pour ![]() Or c’est justement ce qui est demandé …
Or c’est justement ce qui est demandé …
On apprend cependant, avec ce qui précède, que ![]()
D’ailleurs, cette inclusion est nécessairement une égalité dès que ![]() sans quoi
sans quoi ![]() serait un endomorphisme diagonalisable ne possédant qu’une seule valeur propre, donc serait une homothétie … Et ce n’est pas le cas puisque, par exemple :
serait un endomorphisme diagonalisable ne possédant qu’une seule valeur propre, donc serait une homothétie … Et ce n’est pas le cas puisque, par exemple : ![]() n’est pas colinéaire à
n’est pas colinéaire à ![]()
On recherche donc des vecteurs propres associés aux valeurs propres -1 et 1.
Proposons deux stratégies.
Stratégie 1
On observe que, pour tout ![]() :
:
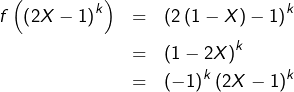
C’est une base de vecteurs propres pour ![]()
Stratégie 2
Posons, pour tout ![]() :
:
![]()
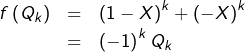

Supposons ![]() nilpotent. Notons
nilpotent. Notons ![]() son indice :
son indice : ![]() et
et ![]() Il existe donc
Il existe donc ![]() tel que
tel que ![]() Comme
Comme ![]() on voit déjà que
on voit déjà que ![]()
Maintenant, si ![]() alors il existe
alors il existe ![]() tel que
tel que ![]() d’où par récurrence :
d’où par récurrence :
![]()
Si ![]() est nilpotent, alors
est nilpotent, alors ![]()
Passons à la réciproque … qui est fausse sans condition sur ![]() Contre-exemple : l’endomorphisme
Contre-exemple : l’endomorphisme ![]() canoniquement associé à
canoniquement associé à
![Rendered by QuickLaTeX.com \[M=\left[\begin{array}{ccc}0 & 0 & 0\\0 & 0 & -1\\0 & 1 & 0\end{array}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fce681109df43660832cd918b66463a7_l3.png)
On a toutefois une réciproque partielle vraie si ![]()
En effet, supposons que ![]() Comme le polynôme caractéristique de
Comme le polynôme caractéristique de ![]() est scindé dans
est scindé dans ![]() (d’après le théorème fondamental de l’algèbre),
(d’après le théorème fondamental de l’algèbre), ![]() est trigonalisable.
est trigonalisable.
Il existe donc une base ![]() de
de ![]() dans laquelle
dans laquelle ![]() est représenté par une matrice de la forme :
est représenté par une matrice de la forme :
![Rendered by QuickLaTeX.com \[T=\left[\begin{array}{cccc}0 & t_{1,2} & \cdots & t_{1,n}\\\vdots & \ddots & \ddots & \vdots\\\vdots & & \ddots & t_{n-1,n}\\0 & \cdots & \cdots & 0\end{array}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4c8e9204df801454e754c467e94d028f_l3.png)

Comme ![]() possède
possède ![]() valeurs propres distinctes, les sev propres sont tous de dimension 1 (on sait en effet que leur somme
valeurs propres distinctes, les sev propres sont tous de dimension 1 (on sait en effet que leur somme ![]() est directe; si l’un d’eux était de dimension
est directe; si l’un d’eux était de dimension ![]() on aurait
on aurait ![]() ce qui est absurde). Pour chaque valeur propre
ce qui est absurde). Pour chaque valeur propre ![]() de
de ![]() notons
notons ![]() la droite propre associée.
la droite propre associée.
Soit ![]() tel que
tel que ![]() Comme
Comme ![]() et
et ![]() commutent, alors
commutent, alors ![]() est stable par
est stable par ![]()
Choisissons un vecteur ![]() Comme
Comme ![]() il existe
il existe ![]() tel que
tel que ![]() d’où
d’où ![]() Or
Or ![]() et donc
et donc ![]() ce qui nous laisse :
ce qui nous laisse :
- si
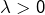 : deux possibilités pour
: deux possibilités pour 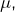 à savoir
à savoir 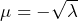 ou
ou 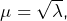
- si
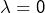 : une seule possibilité, à savoir
: une seule possibilité, à savoir 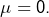
Par conséquent, si l’on note ![]() les valeurs propres de
les valeurs propres de ![]() et
et ![]() une base de vecteurs propres pour
une base de vecteurs propres pour ![]() (avec
(avec ![]() pour tout
pour tout ![]() alors la matrice dans
alors la matrice dans ![]() de
de ![]() est la forme :
est la forme :
![Rendered by QuickLaTeX.com \[\left[\begin{array}{cccc}\pm\sqrt{\lambda_{1}} & 0 & \cdots & 0\\0 & \pm\sqrt{\lambda_{2}} & \ddots & \vdots\\\vdots & \ddots & \ddots & 0\\0 & \cdots & 0 & \pm\sqrt{\lambda_{n}}\end{array}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1d3e6e5e1dd5c7edb2cf60d0e5de27d4_l3.png)
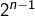 possibilités si
possibilités si 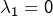
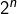 possibilités si
possibilités si 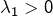
Réciproquement, il est évident que si ![]() est représenté par une telle matrice dans
est représenté par une telle matrice dans ![]() alors
alors ![]()
En résumé …
Proposition
Si ![]() est endomorphisme d’un
est endomorphisme d’un ![]() espace vectoriel
espace vectoriel ![]() de dimension
de dimension ![]() possédant des valeurs propres positives toutes distinctes, alors l’équation
possédant des valeurs propres positives toutes distinctes, alors l’équation ![]() possède
possède ![]() ou
ou ![]() solutions dans
solutions dans ![]() , selon que 0 est ou n’est pas valeur propre de
, selon que 0 est ou n’est pas valeur propre de ![]() .
.
Comme demandé, proposons deux méthodes.
Méthode 1
On commence par observer que, pour tout ![]() :
:
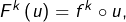 pour tout
pour tout 
- et donc
![Rendered by QuickLaTeX.com \left[P\left(F\right)\right]\left(u\right)=P\left(f\right)\circ u,](https://math-os.com/wp-content/ql-cache/quicklatex.com-7d4ebafe09e295269dc22fb0c6862f50_l3.png) pour tout
pour tout ![Rendered by QuickLaTeX.com P\in\mathbb{R}\left[X\right].](https://math-os.com/wp-content/ql-cache/quicklatex.com-240eab9114be572f4aafbc7eaaa15427_l3.png)
Il en résulte que si ![]() est annulateur de
est annulateur de ![]() alors
alors ![]() est aussi annulateur de
est aussi annulateur de ![]()
En choisissant en outre ![]() scindé dans
scindé dans ![]() et à racines simples (par exemple le polynôme minimal de
et à racines simples (par exemple le polynôme minimal de ![]() on voit (cf. cette CNS) que
on voit (cf. cette CNS) que ![]() est diagonalisable.
est diagonalisable.
Méthode 2
On considère une base ![]() de
de ![]() constituée de vecteurs propres pour
constituée de vecteurs propres pour ![]() :
:
![]()
![]()
![Rendered by QuickLaTeX.com \[ \sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_{i,j}\thinspace\varphi_{i,j}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d085468a36f5562ad41ca3fddb41cae1_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{j=1}^{n}\alpha_{k,j}e_{j}=0_{E}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f5703a8cd5effbc5229b6ec897dc40e3_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left[F\left(\varphi_{i,j}\right)\right]\left(e_{k}\right) & = & \left(f\circ\varphi_{i,j}\right)e_{k}\\& = & \delta_{i,k}\thinspace f\left(e_{j}\right)\\& = & \delta_{i,k}\thinspace\lambda_{j}\thinspace e_{j}\\& = & \lambda_{j}\thinspace\varphi_{i,j}\left(e_{k}\right)\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-2204df1eb3820846ecb0f2b1387a664f_l3.png)
Moralité : la famille ![]() est une base de vecteurs propres pour
est une base de vecteurs propres pour ![]()
Le résultat à démontrer est évident si l’un des deux endomorphismes est une homothétie. On va tâcher de se ramener à cette situation.
Comme ![]() est algébriquement clos, le polynôme caractéristique de
est algébriquement clos, le polynôme caractéristique de ![]() possède au moins une racine complexe; autrement dit :
possède au moins une racine complexe; autrement dit : ![]() possède au moins une valeur propre
possède au moins une valeur propre ![]() .
.
Posons ![]() : c’est le sous-espace vectoriel propre pour
: c’est le sous-espace vectoriel propre pour ![]() associé à la valeur propre
associé à la valeur propre ![]() Evidemment,
Evidemment, ![]() est stable par
est stable par ![]() et l’endomorphisme induit est l’homothétie
et l’endomorphisme induit est l’homothétie ![]() Mais comme
Mais comme ![]() et
et ![]() commutent, alors
commutent, alors ![]() est aussi stable par
est aussi stable par ![]()
Notons ![]() l’endomorphisme induit. A nouveau (comme
l’endomorphisme induit. A nouveau (comme ![]() est algébriquement clos)
est algébriquement clos) ![]() possède au moins une valeur propre
possède au moins une valeur propre ![]()
Pour finir, tout vecteur ![]() vérifiant
vérifiant ![]() est un vecteur propre pour
est un vecteur propre pour ![]() et pour
et pour ![]()

Si ![]() possède au moins une valeur propre, c’est réglé (la droite vectorielle engendrée par un quelconque vecteur propre convient : c’est un sous-espace stable de dimension 1).
possède au moins une valeur propre, c’est réglé (la droite vectorielle engendrée par un quelconque vecteur propre convient : c’est un sous-espace stable de dimension 1).
Supposons désormais que le spectre de ![]() soit vide.
soit vide.
Considérons un polynôme ![]() annulateur de
annulateur de ![]() : rappelons que l’existence d’un tel polynôme découle du fait que la famille
: rappelons que l’existence d’un tel polynôme découle du fait que la famille ![]() est liée, puisque
est liée, puisque ![]() Ce polynôme se décompose en produit de polynômes irréductibles dans
Ce polynôme se décompose en produit de polynômes irréductibles dans ![]() de degré 1 ou 2 :
de degré 1 ou 2 :
![Rendered by QuickLaTeX.com \[ A=\prod_{j=1}^{r}\,A_{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b20f45a049c5c02e8886300691df9259_l3.png)
Posons donc ![]() Soit
Soit ![]() la famille
la famille ![]() est libre car sinon
est libre car sinon ![]() serait un vecteur propre. On considère alors le plan
serait un vecteur propre. On considère alors le plan ![]() il s’agit d’un plan stable puisque si
il s’agit d’un plan stable puisque si ![]() alors :
alors :
![]()

Notons ![]() l’endomorphisme canoniquement associé à
l’endomorphisme canoniquement associé à ![]() Il s’agit de prouver que :
Il s’agit de prouver que :
![]()
Preuve de l’implication 
Notons ![]() les valeurs propres distinctes de
les valeurs propres distinctes de ![]() Alors :
Alors :
![Rendered by QuickLaTeX.com \[\mathbb{C}^{n}=\bigoplus_{i=1}^{q}\ker\left(u-\lambda_{i}\thinspace id\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b14b87983b2a65f0335232835aaf4772_l3.png)
Soit ![]() tel que
tel que ![]() soit nilpotent. Il existe
soit nilpotent. Il existe ![]() tel que
tel que ![]()
Pour tout ![]() et tout
et tout ![]() :
:
![]()
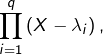 qui n’est autre que le polynôme minimal de
qui n’est autre que le polynôme minimal de De ce fait ![]()
Preuve de l’implication 
Montrons la contraposée. Supposons ![]() non diagonalisable et notons
non diagonalisable et notons ![]() son polynôme minimal (qui est scindé dans
son polynôme minimal (qui est scindé dans ![]() d’après le théorème de d’Alembert-Gauss) :
d’après le théorème de d’Alembert-Gauss) :
![Rendered by QuickLaTeX.com \[\mu=\prod_{i=1}^{q}\left(X-\lambda_{i}\right)^{r_{i}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b2974f13577b805c1413c8d39569a72f_l3.png)
![]()
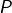 n’est pas annulateur de
n’est pas annulateur de  car c’est un polynôme non nul, de degré
car c’est un polynôme non nul, de degré 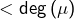 ,
,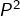 est annulateur de
est annulateur de  car
car 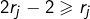 et donc
et donc 
Ainsi ![]() est nilpotent et non nul.
est nilpotent et non nul.
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.

