Solutions détaillées de neuf exercices sur la notion de dimension en algèbre linéaire (fiche 01).
Cliquer ici pour accéder aux énoncés.
Divers éléments théoriques sont disponibles dans cet article.


Selon la formule de Grassmann :
![]()
Il s’ensuit que :
![]()
Si ![]() est une homothétie, il est évident que
est une homothétie, il est évident que ![]() et donc (vu que
et donc (vu que ![]() :
:
![]()
D’après la caractérisation des homothéties, il existe un vecteur ![]() tel que
tel que ![]() soit libre. Cette famille est donc une base de
soit libre. Cette famille est donc une base de ![]()
Considérons l’application :
![]()
➢➢ La linéarité de ![]() est évidente.
est évidente.
➢➢ Injectivité de ![]() :
:
Si ![]() alors
alors ![]() donc
donc ![]() Ceci entraîne que
Ceci entraîne que ![]() est l’endomorphisme nul (une application linéaire qui s’annule sur une base est l’application nulle).
est l’endomorphisme nul (une application linéaire qui s’annule sur une base est l’application nulle).
➢➢ Surjectivité de ![]() :
:
Soit ![]() Décomposons
Décomposons ![]() dans la base
dans la base ![]() sous la forme :
sous la forme :
![]()
![]()
En définitive, ![]() est un isomorphisme. Il en résulte que :
est un isomorphisme. Il en résulte que :
![]()
Considérons la base canonique ![]() de
de ![]() et translatons-la de
et translatons-la de ![]() .
.
Ceci signifie simplement qu’on ajoute la matrice unité à chaque matrice élémentaire pour fabriquer une nouvelle famille de ![]() matrices.
matrices.
Prouvons que la famille ![]() est une base de
est une base de ![]()
Notons ![]() si
si ![]() alors :
alors :
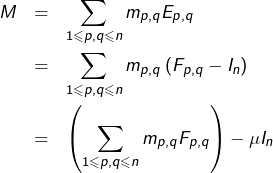
![]()
![Rendered by QuickLaTeX.com \[\sum_{p=1}^{n}F_{p,p}=\left(n+1\right)I_{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-27f6b1eeb8c29e83cd086ab8c093c646_l3.png)
![Rendered by QuickLaTeX.com \[M=\left(\sum_{1\leqslant p,q\leqslant n}m_{p,q}F_{p,q}\right)-\frac{\mu}{n+1}\sum_{p=1}^{n}F_{p,p}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-74702e08a180fede93c52ead79244853_l3.png)
Comme cette famille comporte ![]() matrices, c’est bien une base de
matrices, c’est bien une base de ![]()
Enfin, on constate que les ![]() sont toutes inversibles, puisque ce sont des matrices triangulaires (voire diagonales pour certaines d’entre-elles) dont les termes diagonaux sont tous nuls.
sont toutes inversibles, puisque ce sont des matrices triangulaires (voire diagonales pour certaines d’entre-elles) dont les termes diagonaux sont tous nuls.

Considérons l’application ![]() définie par :
définie par :
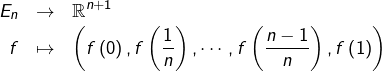
Si ![]() alors
alors ![]() pour tout
pour tout ![]() Et comme la restriction de
Et comme la restriction de ![]() à
à ![]() est affine, elle est nulle et donc
est affine, elle est nulle et donc ![]() Ainsi
Ainsi ![]() est injective.
est injective.
Etant donné ![]() considérons l’application
considérons l’application ![]() définie par :
définie par :
![Rendered by QuickLaTeX.com \[\boxed{\forall x\in\left[0,1\right],\:f_{j}\left(x\right)=\left\{ \begin{array}{ccc}nx-j+1 & \textrm{si} & x\in\left[\frac{j-1}{n},\frac{j}{n}\right]\\\\-nx+j+1 & \textrm{si} & x\in\left[\frac{j}{n},\frac{j+1}{n}\right]\\\\0 & \textrm{sinon}\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0714db450198ee825030be524fdb99e2_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{f_{0}\left(x\right)=\left\{ \begin{array}{ccc}-nx+1 & \textrm{si} & x\in\left[0,\frac{1}{n}\right]\\0 & \textrm{sinon}\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-39dc0970c577d502cd5738b9cdd20e5d_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{f_{n}\left(x\right)=\left\{ \begin{array}{ccc}nx-n+1 & \textrm{si} & \textrm{x}\in\left[\frac{n-1}{n},1\right]\\0 & \textrm{sinon}\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-86842b561c31a434822d0839ea7f5af3_l3.png)
Soit alors ![]() l’application
l’application
![Rendered by QuickLaTeX.com \[f=\sum_{j=0}^{n}\,b_{j}\,f_{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6b37b74930020d24fcbf81a24fa9bd85_l3.png)
![]()
![]()

Notons ![]() une primitive de
une primitive de ![]() (on rappelle que toute application continue d’un intervalle
(on rappelle que toute application continue d’un intervalle ![]() dans
dans ![]() admet des primitives). Soit
admet des primitives). Soit ![]() dérivable et soit :
dérivable et soit :
![]()
![]()
![]()
Remarque
Ce qui précède est fondamental :
Si ![]() est continue, l’espace des solutions sur
est continue, l’espace des solutions sur ![]() de l’équation différentielle
de l’équation différentielle
![]()
Considérons maintenant l’équation différentielle :
![]()
![]()
Ceci permet de se ramener à l’équation différentielle ![]() avec :
avec :
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{x\mapsto\left\{\begin{array}{cc}\lambda_{0}\left(x^{2}-x\right)^{2} & \text{si }x\leqslant0\\\lambda_{1}\left(x^{2}-x\right)^{2} & \text{si }0<x\leqslant1\\\lambda_{2}\left(x^{2}-x\right)^{2} & \text{si }x>1\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-744320554c6203d9bf63d32faf77dad1_l3.png)
Réciproquement, l’application ainsi définie est dérivable quel que soit ![]() et c’est donc une solution sur
et c’est donc une solution sur ![]()
En conclusion :
![]()
![Rendered by QuickLaTeX.com \[\boxed{\varphi_{0}:\mathbb{R}\rightarrow\mathbb{R},\thinspace x\mapsto\left\{ \begin{array}{cc}\left(x^{2}-x\right)^{2} & \text{si }x<0\\0 & \text{sinon} \end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0963a88fc4fa9670a203f6df53df987d_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\varphi_{1}:\mathbb{R}\rightarrow\mathbb{R},\thinspace x\mapsto\left\{ \begin{array}{cc} \left(x^{2}-x\right)^{2} & \text{si }0<x<1\\0 & \text{sinon}\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-40983395a963ac5fa6d3cab31b9190b5_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\varphi_{2}:\mathbb{R}\rightarrow\mathbb{R},\thinspace x\mapsto\left\{ \begin{array}{cc} \left(x^{2}-x\right)^{2} & \text{si }x>1\\0 & \text{sinon}\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3e4786bd9ae12c80f8d135aea5f5569b_l3.png)
Illustration dynamique
L’illustration dynamique ci-dessous permet de visualiser les solutions.
Les trois sliders contrôlent respectivement les coefficients ![]()
![]() et
et ![]()
En positionnant deux de ces trois coefficients à 0, on peut voir le graphe d’une solution proportionnelle à l’une des ![]()
Translater le système de coordonnées en pressant SHIFT →↑↓←.
Zoomer / dézoomer en utilisant les touches P / M.
Notons ![]() la restriction de
la restriction de ![]() à
à ![]() Son noyau et son image sont respectivement :
Son noyau et son image sont respectivement :
![]()
![]()
Le théorème du rang appliqué à ![]() donne :
donne :
(![]() )
) ![]()
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{ccc}\mbox{rg}\left(g\right) & = & n-\dim\left(\ker\left(g\right)\right)\\\\\mbox{rg}\left(f\circ g\right) & = & n-\dim\left(\ker\left(f\circ g\right)\right)\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b01c8de5cee4907754f44ec2f7a7844b_l3.png)
![]()
(![]() )
) ![]()
L’égalité dans ![]() se produit lorsque l’inclusion
se produit lorsque l’inclusion ![]() est une égalité, c’est-à-dire lorsque
est une égalité, c’est-à-dire lorsque ![]()
Passons à la seconde inégalité.
L’inclusion évidente ![]() donne, en passant aux dimensions :
donne, en passant aux dimensions :
![]()
![]()
(![]() )
) ![]()
On peut compléter la famille libre ![]() en une base
en une base
![]()
![]()
![]()
L’expression de toute forme linéaire ![]() dans la base
dans la base ![]() est :
est :
![Rendered by QuickLaTeX.com \[\varphi=\sum_{i=1}^{n}\varphi\left(v_{i}\right)\thinspace v_{i}^{\star}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-59d8519b74960c757803321c984b07c1_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{\bigcap_{i=1}^{r}F_{i}=\text{vect}\left(v_{r+1}^{\star},\cdots,v_{n}^{\star}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dcb3ab1a1265bb863f69e6055fa48c39_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\dim\left(\bigcap_{i=1}^{r}F_{i}\right)=n-r}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c8b29cfffd25037c312e4a71056b149c_l3.png)

Il semble que le plus clair consiste à raisonner matriciellement. Notons :
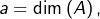
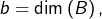
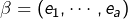 une base de
une base de 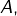 complétée en une base
complétée en une base  de
de 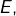
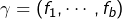 une base de
une base de 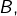 complétée en une base
complétée en une base  de
de 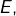
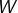 le sous-espace vectoriel de
le sous-espace vectoriel de 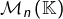 constitué des matrices dont les termes situés en ligne
constitué des matrices dont les termes situés en ligne 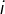 et colonne
et colonne 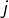 avec
avec 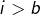 ou
ou 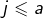 sont tous nuls.
sont tous nuls.
Dans l’illustration ci-dessous, tous les termes de la zone grisée sont nuls, les autres (zone bleutée) sont arbitraires :
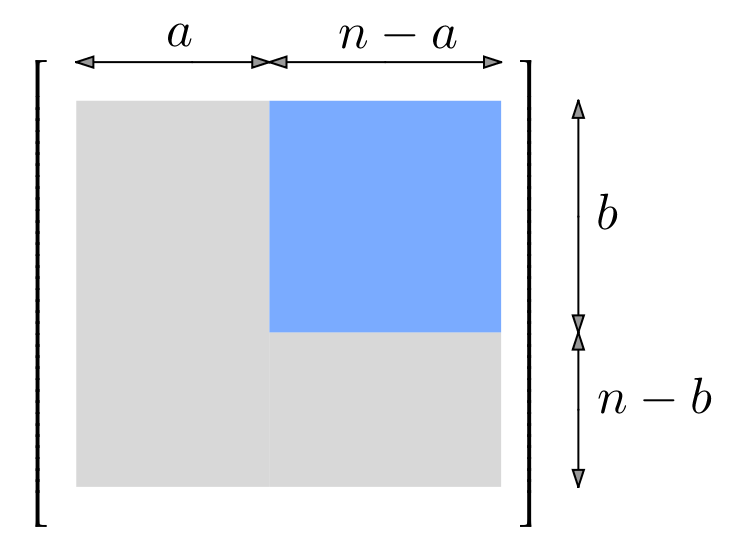
En associant à tout ![]() sa matrice relativement aux bases
sa matrice relativement aux bases ![]() et
et ![]() , on définit une application linéaire de
, on définit une application linéaire de ![]() vers
vers ![]() Cette application est bijective car une application linéaire est entièrement déterminée par la donnée des images des vecteurs d’une base. En outre, si
Cette application est bijective car une application linéaire est entièrement déterminée par la donnée des images des vecteurs d’une base. En outre, si ![]() désigne la base canonique de
désigne la base canonique de ![]() alors la sous famille
alors la sous famille ![]() est une base de
est une base de ![]() et donc
et donc ![]() En conclusion :
En conclusion :
![]()

Bientôt 🙂
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
