icone-math-OS-Exos
exercice 1 facile

On calcule successivement :

    \[\binom{7}{3}=\frac{7\times6\times5}{3\times2}=\fcolorbox{black}{myBlue}{35}\]

puis (avec la formule de symétrie) :

    \[\binom{12}{10}=\binom{12}{2}=\frac{12\times11}{2}=\fcolorbox{black}{myBlue}{66}\]

et enfin :

    \[\binom{8}{4}=\frac{8\times7\times6\times5}{4\times3\times2}=\fcolorbox{black}{myBlue}{70}\]

exercice 2 facile

Fonction de calcul de \displaystyle{\binom{n}{k}} écrite en Python 3 :

def binomial (n, k):
c = 1;
for j in range (k):
    c = (c * (n-j)) // (j+1)
return c

Un exemple :

>>> binomial (15, 4)
1365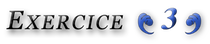

En remplaçant \left(n,k\right) par \left(2n+1,n+1\right) dans la formule du pion :

    \[k\binom{n}{k}=n\binom{n-1}{k-1}\]

on obtient :

    \[\left(n+1\right)\binom{2n+1}{n+1}=\left(2n+1\right)\binom{2n}{n}\]

Ceci montre que :

    \[n+1\mid\left(2n+1\right)\binom{2n}{n}\]

Comme \text{pgcd}\left(n+1,2n+1\right)=1, on conclut avec le théorème de Gauss que :

    \[\boxed{n+1\mid\binom{2n}{n}}\]

Remarque

L’entier \displaystyle{\binom{2n}{n}} est appelé le n-ème coefficient binomial central.

Quant au rationnel :

    \[C_{n}=\frac{1}{n+1}\binom{2n}{n}\]

il s’agit donc un entier. C’est le n-ème nombre de Catalan.

D’après la formule du binôme :

    \[0=\left(1-1\right)^{n}=\sum_{k=0}^{n}\binom{n}{k}\left(-1\right)^{k}\left(1\right)^{n-k}\]

Autrement dit :

    \[\boxed{\sum_{k=0}^{n}\left(-1\right)^{k}\binom{n}{k}=0}\]

Remarque

Il faut bien voir ici le rôle de l’hypothèse n\geqslant1. En effet : \left(1-1\right)^{0}=1.

Passons à une interprétation combinatoire de la formule encadrée. Etant donnés un ensemble E de cardinal n et un entier k\in\left\{0,\cdots,n\right\} , il existe \displaystyle{\binom{n}{k}} parties de E de cardinal k.

Le nombre de parties de E de cardinal pair est :

    \[p_{n}=\sum_{0\leqslant2q\leqslant n}\binom{n}{2q}\qquad\left(\clubsuit\right)\]

tandis que le nombre de parties de cardinal impair est :

    \[i_{n}=\sum_{1\leqslant2q+1\leqslant n}\binom{n}{2q+1}\qquad\left(\spadesuit\right)\]

Or, si l’on note P_{n} (resp. I_{n}) l’ensemble des parties de cardinal pair (resp. impair) de E, et si l’on choisit un élément \alpha\in E (ce qui est possible puisque n\geqslant1), alors l’application :

    \[\varphi_{n}:P_{n}\rightarrow I_{n},\thinspace X\mapsto\left\{\begin{array}{cc}X-\left\{\alpha\right\} & \text{si }\alpha\in X\\X\cup\left\{\alpha\right\} & \text{sinon}\end{array}\right.\]

est une bijection.

Détail (cliquer pour déplier / replier)

Il suffit, pour justifier le caractère bijectif de \varphi_{n}, de considérer l’application

    \[\psi_{n}:I_{n}\rightarrow P_{n},\thinspace X\mapsto\left\{\begin{array}{cc}X-\left\{\alpha\right\} & \text{si }\alpha\in X\\X\cup\left\{\alpha\right\} & \text{sinon}\end{array}\right.\]

et d’observer que

    \[ \varphi_{n}\circ\psi_{n}=id_{I_{n}}\qquad\text{et}\qquad\psi_{n}\circ\varphi_{n}=id_{P_{n}}\]

La première de ces deux relations entraîne la surjectivité de \varphi_{n}, tandis que la seconde entraîne son injectivité.

Il s’ensuit que \text{card}\left(P_{n}\right)=\text{card}\left(I_{n}\right), c’est-à-dire p_{n}=i_{n}. D’après les formules \left(\clubsuit\right) et \left(\spadesuit\right), on voit maintenant que :

    \[\sum_{0\leqslant2q\leqslant n}\binom{n}{2q}-\sum_{1\leqslant2q+1\leqslant n}\binom{n}{2q+1}=0\]

c’est-à-dire :

    \[\sum_{k=0}^{n}\left(-1\right)^{k}\binom{n}{k}=0\]

comme souhaité.

On sait (voir par exemple cet article) que :

    \[\boxed{A_{m,n}=\binom{n+1}{m+1}}\]

Grâce à la formule du pion :

    \[\frac{1}{k}\binom{k}{m}=\frac{1}{m}\binom{k-1}{m-1}\]

donc :

    \[B_{m,n}=\frac{1}{m}\sum_{k=m}^{n}\binom{k-1}{m-1}=\frac{1}{m}A_{m-1,n-1}\]

soit :

    \[\boxed{B_{m,n}=\frac{1}{m}\binom{n}{m}}\]

Toujours d’après la formule du pion :

    \[k\binom{k}{m}=\left(m+1\right)\binom{k+1}{m+1}-\binom{k}{m}\]

donc :

    \begin{eqnarray*}C_{m,n} & = & \left(m+1\right)\sum_{k=m}^{n}\binom{k+1}{m+1}-\sum_{k=m}^{n}\binom{k}{m}\\ & = & \left(m+1\right)A_{m+1,n+1}-A_{m,n} \end{eqnarray*}

soit :

    \[\boxed{C_{m,n}=\left(m+1\right)\binom{n+2}{m+2}-\binom{n+1}{m+1}}\]

Après quelques calculs préalables (pour n=2 puis n=3 : voir les indications), on peut conjecturer la formule suivante, valable pour tout entier n\in\mathbb{N}, toute application g:\mathbb{R}\rightarrow\mathbb{R} et tout x\in\mathbb{R} :

    \[\boxed{\left[F^{n}\left(g\right)\right]\left(x\right)=\sum_{k=0}^{n}\binom{n}{k}g\left(\alpha^{k}\beta^{n-k}x\right)}\]

et l’établir par récurrence. Mais cette démonstration serait en tout point calquée sur celle de la formule du binôme.

Il est nettement plus judicieux de déduire cette formule de celle du binôme, appliquée dans l’anneau des endomorphismes de \mathbb{R}^{\mathbb{R}}.

Pour cela, considérons :

    \[A:\mathbb{R}^{\mathbb{R}}\rightarrow\mathbb{R}^{\mathbb{R}},\thinspace g\mapsto\left[x\mapsto g\left(\alpha x\right)\right]\]

    \[B:\mathbb{R}^{\mathbb{R}}\rightarrow\mathbb{R}^{\mathbb{R}},\thinspace g\mapsto\left[x\mapsto g\left(\beta x\right)\right]\]

On voit facilement que les applications A et B sont linéaires (autrement dit : des endomorphismes de \mathbb{R}^{\mathbb{R}}) et de plus que :

    \[A\circ B=B\circ A\]

En outre F=A+B et donc, pour tout n\in\mathbb{N} :

    \[F^{n}=\sum_{k=0}^{n}\binom{n}{k}A^{k}\circ B^{n-k}\]

La formule annoncée en résulte aussitôt.

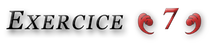
Considérons un ensemble E de cardinal 3n et formons une partition de E en trois sous-ensembles X,Y et Z, chacun de cardinal n. Toute partie F de E de cardinal n est l’union (disjointe) de ses intersections A,B et C avec X,Y et Z respectivement.

Posons :

    \[T=\left\{ \left(A,B,C\right)\in\mathcal{P}\left(X\right)\times\mathcal{P}\left(Y\right)\times\mathcal{P}\left(Z\right);\,\text{card}\left(A\right)+\text{card}\left(B\right)+\text{card}\left(C\right)=n\right\}\]

L’application :

    \[\varphi:\mathcal{P}_{n}\left(E\right)\rightarrow T,\,F\mapsto\left(F\cap X,F\cap Y,F\cap Z\right)\]

est bijective (et sa bijection réciproque est définie par \varphi^{-1}\left(A,B,C\right)=A\cup B\cup C).

Il en résulte :

    \[ \text{card}\left(\mathcal{P}_{n}\left(E\right)\right)=\text{card}\left(T\right)\]

c’est-à-dire :

    \[\boxed{\binom{3n}{n}=\sum_{p=0}^{n}\sum_{q=0}^{n-p}\binom{n}{p}\binom{n}{q}\binom{n}{p+q}}\]

Remarque

Un point de vue équivalent, quoique plus « algébrique », consiste à calculer de deux façons le coefficient de X^{n} dans \left(1+X\right)^{3n}.

Fixons \left(x,y\right)\in\mathbb{R}^{2} et montrons de deux manières que, pour tout n\in\mathbb{N} :

    \[\boxed{\left(x+y\right)_{n}=\sum_{k=0}^{n}\binom{n}{k}\left(x\right)_{k}\left(y\right)_{n-k}}\]

Solution 1 : par récurrence (cliquer pour déplier / replier)

Pour n=0, les deux membres valent 1 par définition. Supposons l’égalité vraie pour un certain n\in\mathbb{N}. Alors :

    \[\left(x+y\right)_{n+1}=\left(x+y\right)_{n}\left(x+y-n\right)\]


En écrivant artificiellement :

    \[x+y-n=\left(x-k\right)+\left(y-n+k\right)\]


il vient :

    \begin{eqnarray*} \left(x+y\right)_{n+1} & = & \sum_{k=0}^{n}\binom{n}{k}\left(x\right)_{k}\left(x-k\right)\left(y\right)_{n-k}+\sum_{k=0}^{n}\binom{n}{k}\left(x\right)_{k}\left(y\right)_{n-k}\left(y-n+k\right)\\& = & \sum_{k=0}^{n}\binom{n}{k}\left(x\right)_{k+1}\left(y\right)_{n-k}+\sum_{k=0}^{n}\binom{n}{k}\left(x\right)_{k}\left(y\right)_{n+1-k}\end{eqnarray*}


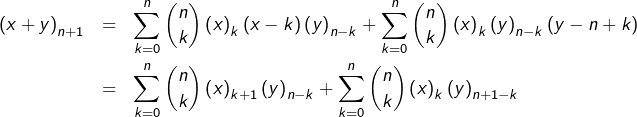
En posant j=k+1 dans l’avant-dernière somme, on obtient :

    \[\left(x+y\right)_{n+1}=\sum_{j=1}^{n+1}\binom{n}{j-1}\left(x\right)_{j}\left(y\right)_{n-j+1}+\sum_{k=0}^{n}\binom{n}{k}\left(x\right)_{k}\left(y\right)_{n+1-k}\]


On isole alors le terme d’indice j=n+1 dans la première somme et celui d’indice k=0 dans la seconde :

    \[\left(x+y\right)_{n+1}=\left(x\right)_{n+1}+\left(y\right)_{n+1}+\sum_{k=1}^{n}\left[\binom{n}{k-1}+\binom{n}{k}\right]\left(x\right)_{k}\left(y\right)_{n+1-k}\]


Finalement, d’après la formule de Pascal :

    \[\left(x+y\right)_{n+1}=\sum_{k=0}^{n+1}\binom{n+1}{k}\left(x\right)_{k}\left(y\right)_{n+1-k}\]


comme souhaité.

Solution 2 : via le lemme énoncé en fin de cet article (cliquer pour déplier / replier)

Posons, pour tout \left(p,q\right)\in\mathbb{N}^{2} :

    \[T_{p,q}=\left(x\right)_{p}\left(y\right)_{q}\left(1+t\right)^{x-p+y-q}\]


où t\in\mathbb{R} est arbitraire. On observe que :

    \begin{eqnarray*}\frac{d}{dt}\left(T_{p,q}\right) & = & \left[\left(x\right)_{p+1}\left(y\right)_{q}+\left(x\right)_{p}\left(y\right)_{q+1}\right]\left(1+t\right)^{x-p+y-q-1}\\& = & \left(x\right)_{p+1}\left(y\right)_{q}\left(1+t\right)^{x-\left(p+1\right)+y-q}+\left(x\right)_{p}\left(y\right)_{q+1}\left(1+t\right)^{x-p+y-\left(q+1\right)}\\& = & T_{p+1,q}+T_{p,q+1}\end{eqnarray*}


Notons f la dérivation par rapport à t et appliquons le lemme. Il vient :

    \[\frac{d^{n}}{dt^{n}}\left(T_{0,0}\right)=\sum_{k=0}^{n}\binom{n}{k}T_{k,n-k}\]

Or :

    \[T_{0,0}=\left(1+t\right)^{x+y}\]


et donc :

    \begin{eqnarray*}\left(x+y\right)_{n}\left(1+t\right)^{x+y-n} & = & \sum_{k=0}^{n}\binom{n}{k}\left(x\right)_{k}\left(y\right)_{n-k}\left(1+t\right)^{x-k+y-\left(n+k\right)}\\& = & \left(\sum_{k=0}^{n}\binom{n}{k}\left(x\right)_{k}\left(y\right)_{n-k}\right)\left(1+t\right)^{x+y-n}\end{eqnarray}


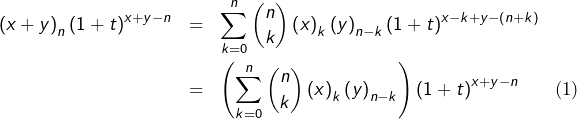
Il reste à simplifier pour conclure que :

    \[\boxed{\left(x+y\right)_{n}=\sum_{k=0}^{n}\binom{n}{k}\left(x\right)_{k}\left(y\right)_{n-k}}\]

exercice 9 difficile

On sait que :

    \[p!\binom{n}{p}=n\left(n-1\right)\cdots\left(n-p+1\right)\qquad\left(\star\right)\]

Soit i l’unique élément de \llbracket0,p-1\rrbracket tel que p\mid n-i.

On voit que :

    \[\frac{n-i}{p}\in\mathbb{N}\qquad\text{et}\qquad\frac{n-i}{p}\leqslant\frac{n}{p}<\frac{n-i+p}{p}\]

et donc :

    \[\frac{n-i}{p}=\left\lfloor \frac{n}{p}\right\rfloor\]


Posons :

    \[A=\prod_{{0\leqslant j<p\atop j\neq i}}\left(n-j\right)\]

L’égalité \left(\star\right) peut s’écrire :

    \[\boxed{\left(p-1\right)!\thinspace\binom{n}{p}=A\left\lfloor \frac{n}{p}\right\rfloor }\]

Comme \left(p-1\right)! et A ne sont pas multiples de p, on conclut que les valuations p-adiques des entiers \binom{n}{p} et \left\lfloor \frac{n}{p}\right\rfloor sont égales.

Remarque

Cette question a fait l’objet du challenge n° 30.

Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.

Partager cet article
    

Laisser un commentaire