icone-challenge-math-OS

Solution pour le challenge 80

Dans ce qui suit, \mathcal{P}\left(\mathbb{N}\right) désigne l’ensemble des parties (sous-ensembles) de \mathbb{N} et \mathfrak{S}\left(\mathbb{N}\right) désigne l’ensemble des permutations de \mathbb{N} (bijections de \mathbb{N} vers lui-même).

Considérons l’application f:\mathfrak{S}\left(\mathbb{N}\right)\rightarrow\mathcal{P}\left(\mathbb{N}\right) qui a tout \sigma\in\mathfrak{S}\left(\mathbb{N}\right) fait correspondre l’ensemble de ses points fixes. Si l’on prouve que f est surjective, il en résultera que \mathfrak{S}\left(\mathbb{N}\right) est non dénombrable, puisque \mathcal{P}\left(\mathbb{N}\right) est non dénombrable.

Soit F\subset\mathbb{N}.

➡ Si \mathbb{N}-F est fini, on considère un cycle c de support \mathbb{N}-F : c’est une permutation dont l’ensemble des points fixes est F. EDIT : Ceci est valable lorsque \mathbb{N}-F est de cardinal au moins 2. Si \mathbb{N}-F=\emptyset, autrement dit si F=\mathbb{N}, pas de problème puisque \mathbb{N} est l’ensemble des points fixes de id_{\mathbb{N}}. Mais si \mathbb{N}-F est un singleton (autrement dit, si F=\mathbb{N}-\{a\} pour un certain a\in\mathbb{N}), alors il n’existe aucune permutation ayant F comme ensemble de points fixes ! Il faut donc rectifier et considérer plutôt f:\mathfrak{S}\left(\mathbb{N}\right)\rightarrow\mathcal{P}\left(\mathbb{N}\right)-\{\mathbb{N}-\{a\};\,a\in\mathbb{N}\}. Comme \{\mathbb{N}-\{a\};\,a\in\mathbb{N}\} est dénombrable, l’ensemble d’arrivée de f reste non dénombrable et la preuve est « réparée » (merci à G. Bigon pour sa remarque). End EDIT

➡ Et sinon, numérotons \mathbb{N}-F en une suite \left(u_{n}\right) strictement croissante et considérons \sigma:\mathbb{N}\rightarrow\mathbb{N} définie par :

    \[\forall p\in F,\thinspace\sigma\left(p\right)=p\]

    \[\forall n\in\mathbb{N},\thinspace\sigma\left(u_{n}\right)=\left\{ \begin{array}{cc}u_{n+1} & \text{si }n\text{ pair}\\u_{n-1} & \text{sinon}\end{array}\right.\]

On constate que \sigma\in\mathfrak{S}\left(\mathbb{N}\right) (c’est une involution) et que f\left(\sigma\right)=F.

Autre point de vue …

Afin de montrer que l’ensemble des permutations de \mathbb{N} n’est pas dénombrable, il suffit de construire une bijection entre une partie non dénombrable de \mathcal{P}\left(\mathbb{N}\right) et \mathfrak{S}\left(\mathbb{N}\right). On commence par partitionner\mathcal{P}\left(\mathbb{N}\right) sous la forme :

    \[\mathcal{P}\left(\mathbb{N}\right)=F\cup I_{f}\cup I_{\infty}\]

où F, I_{f} et I_{\infty} désignent respectivement :

  • l’ensemble des parties finies de \mathbb{N}
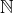
  • l’ensemble des parties infinies de 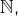\mathbb{N}, dont le complémentaire est fini
  • l’ensemble des parties infinies de 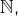\mathbb{N}, dont le complémentaire est infini

On constate que :

➡ F est dénombrable. En effet, si l’on note F_{p} l’ensemble des parties finies, non vides, de \mathbb{N} dont le plus grand élément est p, alors :

    \[F=\left\{ \emptyset\right\} \cup\bigcup_{p=0}^{\infty}F_{p}\]

or chaque F_{p} est fini (de cardinal 2^{p} : on détermine un élément de F_{p} en réunissant \left\{ p\right\} avec une partie de \left\llbracket 0,p-1\right\rrbracket ).

➡ I_{f} est aussi dénombrable. En effet, l’involution

    \[\mathcal{P}\left(\mathbb{N}\right)\rightarrow\mathcal{P}\left(\mathbb{N}\right),X\mapsto\mathbb{N}-X\]

induit une bijection de F sur I_{f}.

Comme \mathcal{P}\left(\mathbb{N}\right) n’est pas dénombrable, ce qui précède prouve que I_{\infty} ne l’est pas non plus.

On considère alors l’application \varphi:I_{\infty}\rightarrow\mathfrak{S}\left(\mathbb{N}\right), qui a toute partie A de \mathbb{N}, infinie et de complémentaire infini, associe la permutation \sigma_{A} définie comme suit :

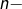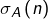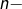  • si n désigne le n-ème entier naturel pair, alors \sigma_{A}\left(n\right) = le n-ème élément de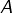 A
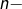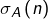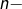  • si n désigne le n-ème entier naturel impair, alors \sigma_{A}\left(n\right) = le n-ème élément de \mathbb{N}-A

Par construction, \sigma_{A} est une permutation de \mathbb{N}.

De plus, \varphi est bijective puisque, si l’on définit

    \[\psi:\mathfrak{S}\left(\mathbb{N}\right)\rightarrow I_{\infty},\thinspace\sigma\mapsto\sigma\left\langle 2\mathbb{N}\right\rangle\]

alors \psi\circ\varphi=id_{I_{\infty}} et \varphi\circ\psi=id_{\mathfrak{S}\left(\mathbb{N}\right)}.

A titre indicatif, voici trois exemples de permutations \sigma_{A}, où A désigne une partie de \mathbb{N}, infinie et de complémentaire infini :

si A est l’ensemble des entiers impairs :

    \[\left(\begin{array}{ccccccccccccccc}0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & \cdots\\1 & 0 & 3 & 2 & 5 & 4 & 7 & 6 & 9 & 8 & 11 & 10 & 13 & 12 & \cdots\end{array}\right)\]

si A est l’ensemble des puissances de 2 :

    \[\left(\begin{array}{ccccccccccccccc}0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & \cdots\\1 & 0 & 2 & 3 & 4 & 5 & 8 & 6 & 16 & 7 & 32 & 9 & 64 & 10 & \cdots\end{array}\right)\]

si A est l’ensemble des nombres premiers :

    \[\left(\begin{array}{ccccccccccccccc}0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & \cdots\\2 & 0 & 3 & 1 & 5 & 4 & 7 & 6 & 11 & 8 & 13 & 9 & 17 & 10 & \cdots\end{array}\right)\]

Pour consulter l’énoncé, c’est ici

Partager cet article
    

Cet article a 4 commentaires

  1. Guillaume Bigon 14 Août 2023 Répondre

    Bonjour,
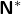    A propos de la première solution, il me semble que \mathbf{N^*} ne possède pas d’antécédent, ainsi que tous les ensembles de la forme A_a=\mathbf{N}-\left\{a\right\}, car une permutation ne peut pas laisser fixes tous les entiers sauf un seul.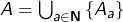
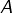    En revanche, si on note A=\bigcup_{a \in \mathbf{N}} \left\{A_a\right\}. A est dénombrable et votre application est bien surjective dans 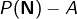P(\mathbf{N})-A qui est non dénombrable.
    J’aime bien l’autre preuve 🙂

    1. René Adad 14 Août 2023 Répondre

      Vous avez raison, une partie de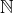 \mathbb{N} de la forme 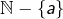\mathbb{N}-\{a\} ne peut pas être l’ensemble des points fixes d’une permutation ! Je m’empresse de rectifier. Et bien sûr vous ne vouliez pas parler de 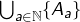\bigcup_{a\in\mathbb{N}}\{A_a\} (qui n’est autre que 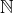\mathbb{N}) mais plutôt de \{A_a;\,a\in\mathbb{N}\}.

      1. Guillaume Bigon 14 Août 2023 Répondre

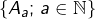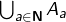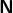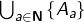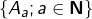        J’ai un doute. Je suis d’accord sur le fait que \bigcup_{a \in \mathbf{N}}A_a vaut \mathbf{N}, mais je ne vois pas bien la différence entre \bigcup_{a \in \mathbf{N}}\left\{A_a\right\} et \left\{A_a ; a \in \mathbf{N}\right\}. Ces deux derniers ensembles possèdent bel et bien les mêmes éléments, n’est ce pas ?

        1. René Adad 14 Août 2023 Répondre

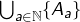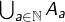          Au temps pour moi … erreur de lecture : j’ai pris \bigcup_{a\in\mathbb{N}}\{A_a\} pour \bigcup_{a\in\mathbb{N}}A_a … Désolé pour le bruit.

Laisser un commentaire