Solution pour le challenge 73
La construction qui suit met en valeur l’idée selon laquelle on résout parfois plus simplement une question en augmentant la dimension de l’espace ambiant.
Posons, pour tout ![]() :
:
![]()
Il est clair que ![]() est une famille non dénombrable de parties de
est une famille non dénombrable de parties de ![]() non dénombrables et deux à deux disjointes.
non dénombrables et deux à deux disjointes.
Par ailleurs, on sait qu’il existe une bijection ![]()
Détail (cliquer pour déplier / replier)
L’équipotence de ![]() et
et ![]() peut être justifiée comme suit.
peut être justifiée comme suit.
On note ![]() pour indiquer que les ensembles
pour indiquer que les ensembles ![]() et
et ![]() sont équipotents (c’est-à-dire : en bijection l’un avec l’autre).
sont équipotents (c’est-à-dire : en bijection l’un avec l’autre).
On sait que si ![]() est infini et si
est infini et si ![]() alors
alors ![]()
Il en résulte que ![]()
Or ![]() et donc
et donc ![]()
Pour les détails, on pourra se reporter à cet article.
Il suffit alors de poser, pour tout ![]() :
:
![]()
![]()
Pour consulter l’énoncé, c’est ici


Voici une bijection explicite de R dans R^2 :
Pour tout réel x, notons (xn) la suite d’entiers de son développement en fraction continue (si x est rationnel, on complète la suite qui est alors finie avec une infinité de 0). On sait que cette suite existe et est unique.
Considérons alors l’application qui à tout réel x associe le couple de réels (y,z) avec y le réel qui admet le développement (x_2n) et z le développement (x_2n+1). Cette application est bien définie et bijective car on sait aussi qu’à toute suite d’entier correspond effectivement un réel (cela découle du fait que la suite des fractions réduites converge).
On peut même généraliser et donner une bijection de R dans R^N (les suites de réels) :
On pose l’application qui à tout réel x représenté par la suite d’entiers de sa fraction continue (xn) associe la suite de réels (zi) où zi est le réel dont la suite d’entiers est formé de la manière suivante : pour z1 on prend les xn d’indice pairs, pour z2 les indices multiples de 3 non divisible par 2, pour z2 les indices multiples de 5 non divisibles par 2 et 3 etc.
Merci pour votre contribution.
Merci pour votre réponse. Je ne l’avais pas vue tout de suite, parce que je pensais que je recevrai automatiquement un mail pour m’avertir (il me semble que c’était comme ça les autres fois). En fait, mon idée de bijection de R² sur R était d’alterner les décimales des deux nombres de départ (sans passer par le développement en base 2, ce qui ne change pas grand chose finalement). Mais je me suis rendu compte que ça marchait moyennement du fait qu’on doive interdire qu’une partie décimale « se termine » par une infinité de 9. Par exemple 9090,90909090… devrait avoir pour antécédent (99,9999… ; 0), c’est-à-dire (100 ; 0), mais l’image de ce couple est en fait 100000. Du coup, c’est pour ça que je vous ai posé la question. Mais ne vous cassez pas la tête, c’était juste par curiosité. J’imagine que cette question a bien dû être résolue, peut-être d’une façon très différente.
Bonjour. Avez-vous un exemple de bijection explicite pas trop alambiquée de R² sur R ?
Bonne question …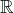 est équipotent à
est équipotent à 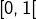 , il suffit de construire une bijection de
, il suffit de construire une bijection de 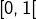 vers
vers 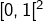 .
.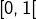 est en bijection avec l’ensemble des suites binaires (à termes dans
est en bijection avec l’ensemble des suites binaires (à termes dans 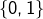 ) dont les termes ne valent pas tous 1 APCR : il suffit d’associer à chaque
) dont les termes ne valent pas tous 1 APCR : il suffit d’associer à chaque 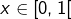 son développement propre en base 2.
son développement propre en base 2.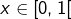 , on note
, on note 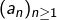 la suite de ses chiffres binaires et on lui associe le couple
la suite de ses chiffres binaires et on lui associe le couple 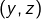 défini par les suites extraites
défini par les suites extraites 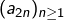 et
et 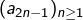 .
.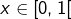 est
est 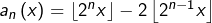 , nous avons une bijection :
, nous avons une bijection :
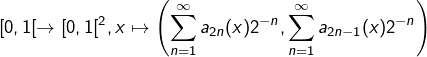
Vu que
Par ailleurs,
Cela dit, on prend
Plus formellement, et vu que le n-ème chiffre binaire de
Je ne vois pas moins alambiqué … et j’espère ne pas avoir raconté de bêtises.
Bon … je me réponds à moi-même … il y a quand même un souci dans ma soi-disant bijection en raison de la non-unicité du développement binaire.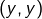 avec
avec 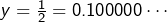 (écriture binaire), alors on a aussi
(écriture binaire), alors on a aussi 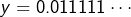 et donc quatre antécédents, à savoir :
et donc quatre antécédents, à savoir :
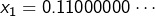
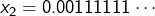
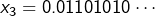
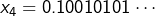
Par exemple, si l’on considère le couple
Bref, il faut encore réfléchir …