Solution pour le challenge 40
Solution 1
Supposons l’existence d’une application continue et injective ![]() et considérons alors :
et considérons alors :
![]()
Conceptuellement, ![]() permet de suivre l’évolution des valeurs prises par
permet de suivre l’évolution des valeurs prises par ![]() lorsqu’on l’applique à un point parcourant le cercle unité. On va constater qu’un problème surgit lorsqu’on effectue un tour complet …
lorsqu’on l’applique à un point parcourant le cercle unité. On va constater qu’un problème surgit lorsqu’on effectue un tour complet …
Comme les trois applications ![]() ,
, ![]() et
et ![]() sont continues, il en va de même pour
sont continues, il en va de même pour ![]() .
.
En outre, l’application
![]()
Détail
L’injectivité de ![]() est intuitivement claire : lorsque
est intuitivement claire : lorsque ![]() parcourt
parcourt ![]() , le couple
, le couple ![]() fait le tour du cercle unité, sans passer deux fois par la même position !
fait le tour du cercle unité, sans passer deux fois par la même position !
Cela dit, nous allons prouver l’injectivité de ![]() de manière rigoureuse.
de manière rigoureuse.
Soient ![]() tels que
tels que ![]() , c’est-à-dire :
, c’est-à-dire :
![]()
![]()
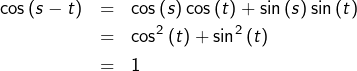
Ainsi ![]() comme souhaité.
comme souhaité.
On va maintenant invoquer le théorème suivant :
Théorème
Si ![]() est un intervalle de
est un intervalle de ![]() et si
et si ![]() est continue et injective, alors
est continue et injective, alors ![]() est strictement monotone.
est strictement monotone.
Ce théorème s’applique à ![]() , qui est donc strictement monotone.
, qui est donc strictement monotone.
Si par exemple ![]() est strictement croissante, alors pour tout
est strictement croissante, alors pour tout ![]() :
:
![]()
![]()
En particulier ![]() , c’est-à-dire
, c’est-à-dire ![]() ce qui est absurde.
ce qui est absurde.
On obtient une contradiction similaire dans le cas où ![]() serait strictement décroissante.
serait strictement décroissante.
En conclusion, il n’existe aucune application continue et injective de ![]() dans
dans ![]() .
.
Remarque 1
L’application ![]() n’est pas injective puisque
n’est pas injective puisque ![]() .
.
Ceci explique qu’on ait dû exclure ![]() de son intervalle de départ et considérer plutôt
de son intervalle de départ et considérer plutôt ![]() .
.
Remarque 2
Des applications continues et injectives de ![]() dans
dans ![]() , il en existe (à commencer par l’identité) !
, il en existe (à commencer par l’identité) !
On vient de voir qu’il n’en existe aucune de ![]() dans
dans ![]() .
.
Et de ![]() dans
dans ![]() , vous en pensez-quoi ? Et plus généralement de
, vous en pensez-quoi ? Et plus généralement de ![]() dans
dans ![]() ?
?
Solution 2, proposée par Shika (élève de terminale !)
Supposons l’existence d’une application continue et injective ![]() dans
dans ![]()
Celle-ci induit alors une bijection continue ![]() de
de ![]() (le cercle unité de
(le cercle unité de ![]() sur une partie non vide, compacte et connexe de
sur une partie non vide, compacte et connexe de ![]() c’est-à-dire un segment
c’est-à-dire un segment ![]() avec
avec ![]()
![]() est un homéomorphisme car pour tout fermé
est un homéomorphisme car pour tout fermé ![]() de
de ![]()
![]() est l’image directe d’une partie compacte par une application continue, donc un compact contenu dans
est l’image directe d’une partie compacte par une application continue, donc un compact contenu dans ![]() donc un fermé de
donc un fermé de ![]()
Etant donné ![]() posons :
posons : ![]()
Les ensembles ![]() et
et ![]() sont homéomorphes; pourtant le premier est connexe mais ce n’est pas le cas du second.
sont homéomorphes; pourtant le premier est connexe mais ce n’est pas le cas du second.
Cette contradiction montre qu’il n’existe aucune application continue et injective de ![]() dans
dans ![]()
Pour consulter l’énoncé, c’est ici

