Solution pour le challenge n° 39

Solution pour le challenge 39

La première chose à faire est sans doute un dessin.

Sur la figure ci-dessous, sont dessinées les deux paraboles d’équations respectives :

$\begin{matrix}y&=&10-x^{2}&\fcolorbox{red}{gray!30}{$\mathcal{P}$}\\\\x&=&4-y^{2}&\fcolorbox{blue}{gray!30}{$\mathcal{Q}$}\end{matrix}$

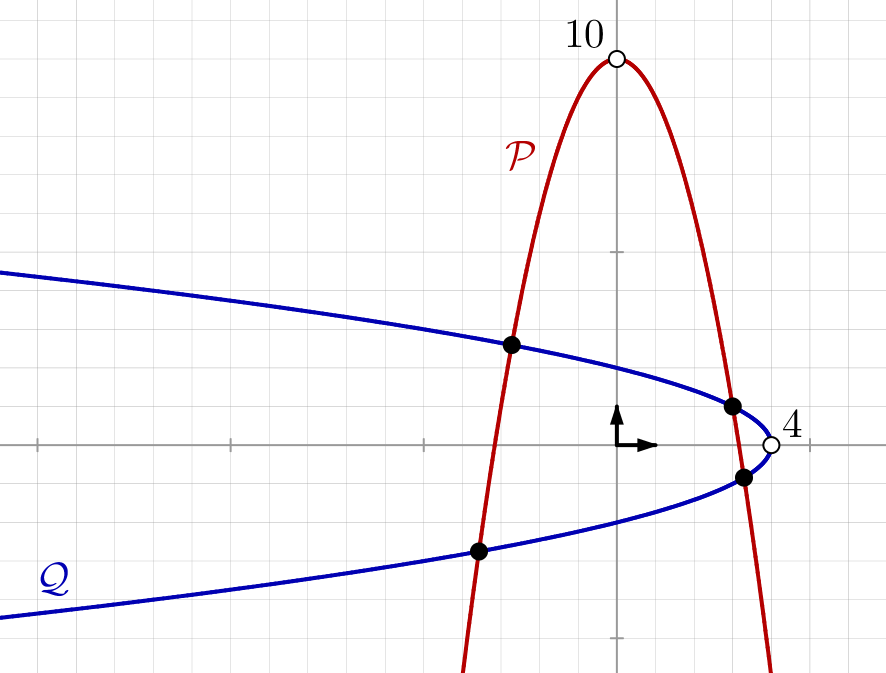
On dénombre quatre points d’intersection, qui sont autant de solutions pour notre système.

Bien sûr, cette simple lecture graphique ne constitue pas une preuve valide, quand bien même elle nous convainc de la réponse (du moins pour la première question). Alors que faire ?

On peut déjà remplacer le système proposé par le système équivalent :

$\left\{\begin{array}{ccc}\left(4-y^{2}\right)^{2}+y-10 & = & 0\\x & = & 4-y^{2}\end{array}\right.$

c’est-à-dire :

$\left\{\begin{array}{ccccc}y^{4}-8y^{2}+y+6 & = & 0 & & \left(\star\right)\\x & = & 4-y^{2}\end{array}\right.$

On observe maintenant que $y=1$ est solution de l’équation $\left(\star\right)$ , à laquelle est associé $x=3$ .

Vous aviez peut-être détecté, depuis le début, que le couple $\left(x,y\right)=\left(3,1\right)$ convient, puisque :

$\left\{\begin{array}{ccc}3^{2}+1 & = & 10\\3+1^{2} & = & 4\end{array}\right.$

Mais alors l’équation $\left(\star\right)$ se factorise (voir par exemple cet article) sous la forme :

$\left(y-1\right)\left(y^{3}+y^{2}-7y-6\right)=0$

A ce stade, on peut envisager (au moins) deux approches …

Approche 1 (cliquer pour déplier / replier)

Si l’on pose pour tout $y\in\mathbb{R}$ :

$f\left(y\right)=y^{3}+y^{2}-7y-6$

il est facile d’étudier le sens de variations de $f$ (sa dérivée est un polynôme du second degré) et de constater qu’il existe des réels

$\alpha=\frac{-1-\sqrt{22}}{3}$

$\beta=\frac{-1+\sqrt{22}}{3}$

tels que $f$ soit strictement croissante sur $\left]-\infty,\alpha\right]$ , strictement décroissante sur $\left[\alpha,\beta\right]$ et de nouveau strictement croissante sur $\left[\beta,+\infty\right[$ .

En outre :

$f\left(\alpha\right)=\frac{-97+44\sqrt{22}}{27}>0$

$f\left(\beta\right)=\frac{-97-44\sqrt{22}}{27}<0$

Comme les limites de $f$ en $-\infty$ et en $+\infty$ valent respectivement $-\infty$ et $+\infty$ , un corollaire bien connu du théorème des valeurs intermédiaires montre que $f$ s’annule exactement trois fois.

Ces calculs sont assez lourds, techniquement parlant… et l’on peut faire plus simple !

Approche 2 (cliquer pour déplier / replier)

Il suffit d’observer que :

$\left\{\begin{array}{ccc}f\left(-3\right) & = & -3\\f\left(-2\right) & = & 4\end{array}\right.$

d’où

$\exists y_{1}\in\left]-3,2\right[;\thinspace f\left(y_{1}\right)=0$

$\left\{\begin{array}{ccc}f\left(-1\right) & = & 1\\f\left(0\right) & = & -6\end{array}\right.$

d’où

$\exists y_{2}\in\left]-1,0\right[;\thinspace f\left(y_{2}\right)=0$

$\left\{\begin{array}{ccc}f\left(2\right) & = & -8\\f\left(3\right) & = & 9\end{array}\right.$

d’où

$\exists y_{3}\in\left]2,3\right[;\thinspace f\left(y_{3}\right)=0$

Vu que l’équation

$y^{3}+y^{2}-7y-6=0$

ne peut pas posséder plus de trois solutions, ceci montre qu’elle en possède exactement trois.

En posant $x_{i}=4-y_{i}^{2}$ pour chaque $i\in\llbracket1,3\rrbracket$ , on obtient trois couples solutions $\left(x_{1},y_{1}\right)$ , $\left(x_{2},y_{2}\right)$ et $\left(x_{3},y_{3}\right)$ , auxquels s’ajoute le couple $\left(3,1\right)$ .

D’une manière ou d’une autre, on voit que notre système possède dans $\mathbb{R}^{2}$ quatre couples solutions, parmi lesquels $\left(3,1\right)$ . Vérifions que seul ce dernier appartient à $\mathbb{Q}^{2}$ .

Pour cela, il suffit d’appliquer le test des racines rationnelles à l’équation :

$y^{3}+y^{2}-7y-6=0\qquad\left(\blacksquare\right)$

Supposons qu’un rationnel $p/q$ soit solution de $(\blacksquare)$ , avec $p\in\mathbb{Z}$ et $q\in\mathbb{N}^{\star}$ premiers entre eux. Alors :

$p\mid1\quad\text{et}\quad q\mid-6$

ce qui impose :

$p\in\left\{-1,1\right\}\quad\text{et}\quad q\in\left\{1,2,3,6\right\}$

Une éventuelle solution rationnelle de $\left(\blacksquare\right)$ doit figurer dans la courte liste :

$1,\frac{1}{2},\frac{1}{3},\frac{1}{6},-1,-\frac{1}{2},-\frac{1}{3},-\frac{1}{6}$

Or, il s’avère (bon … il faut bien calculer un peu …) qu’aucun de ces huit rationnels n’est solution de $\left(\blacksquare\right)$ . Ceci prouve que cette équation ne possède aucune solution rationnelle. Le système proposé possède donc $\left(1,3\right)$ pour seule solution dans $\mathbb{Q}^{2}$ .

Pour consulter l’énoncé, c’est ici

Partager cet article

La publication a un commentaire

Martin Barts--Bérard 14 Mar 2020 Répondre

Problème très intéressant, merci! J’ai appris une nouvelle méthode : le test des racines rationnelles!
Bien à vous

Martin

La publication a un commentaire

Laisser un commentaire Annuler la réponse