Solution pour le challenge 35
On pose pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[H_{n}=\sum_{k=1}^{n}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1e9e62ff52597157f7ef82d4b070212a_l3.png)
![Rendered by QuickLaTeX.com \[K_{n}=\sum_{p=1}^{n}\left(\sum_{k=p}^{n}\frac{1}{k}\right)^{2}+\sum_{k=1}^{n}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-562b18a42e3cb9fb0bd750faf0935b13_l3.png)
![Rendered by QuickLaTeX.com \[K_{n}=H_{n}+\sum_{p=1}^{n}\left(H_{n}-H_{p-1}\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d504858873260dfb1c91fcac13a2c290_l3.png)
Pour commencer, notons :
![Rendered by QuickLaTeX.com \[S_{n}=\sum_{p=1}^{n}H_{p}\quad\text{et}\quad T_{n}=\sum_{p=1}^{n}H_{p}^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-59ab9345e1a51b89ec2990ea9f0320b6_l3.png)
Pour ![]() on intervertit deux
on intervertit deux ![]() sur un domaine triangulaire :
sur un domaine triangulaire :
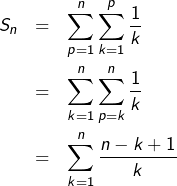
Ainsi :
![]()
Pour ![]() on effectue une transformation d’Abel du type :
on effectue une transformation d’Abel du type :
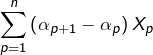
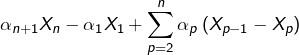
ce qui donne, en remplaçant ![]() et
et ![]() par
par ![]() et
et ![]() respectivement :
respectivement :
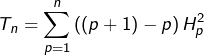
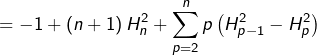
Or, pour tout ![]() :
:
![]()
![]()
donc :
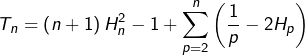
![]()
![]()
soit finalement :
![]()
A présent, on combine le tout (rappelons qu’on a posé ![]() ) :
) :
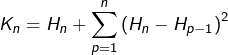
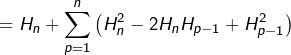
![]()
Or, d’après ce qui précède :
![]()
et :
![]()
![]()
d’où :![]()
![]()
Après simplification, il reste :
![]()
Pour consulter l’énoncé, c’est ici

