Question
Comment résoudre l’équation suivante ?
![]()
Réponse
Il s’agit d’une équation algébrique du troisième degré. Posons, pour tout ![]() :
:
![]()
A un niveau élémentaire, on ne demande en exercice la résolution dans ![]() de telles équations que si elles possèdent au moins une solution « évidente » ou, à la rigueur, rationnelle (voir à ce sujet le test des racines rationnelles dans cet article).
de telles équations que si elles possèdent au moins une solution « évidente » ou, à la rigueur, rationnelle (voir à ce sujet le test des racines rationnelles dans cet article).
Mais ce n’est pas le cas ici ! En effet, si ![]() , alors de deux choses l’une :
, alors de deux choses l’une :
- Si
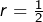 ou
ou 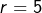 , alors d’évidence
, alors d’évidence 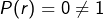 .
. - Si
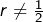 et
et 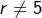 alors
alors 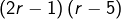 est un rationnel non nul, tandis que
est un rationnel non nul, tandis que 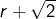 est irrationnel et donc
est irrationnel et donc 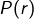 est irrationnel et, en particulier, différent de 1.
est irrationnel et, en particulier, différent de 1.
Dans tous les cas : ![]() .
.
Cela dit, l’étude des variations de la fonction ![]() montre qu’elle est croissante sur
montre qu’elle est croissante sur ![]() , décroissante sur
, décroissante sur ![]() et à nouveau croissante sur
et à nouveau croissante sur ![]() , avec :
, avec :
![]()
![]()
On peut montrer en utilisant une dichotomie que :
![]()
La résolution explicite est possible (comme pour toute équation du troisième degré) mais les formules donnant les solutions sont compliquées et ne présentent pas vraiment d’intérêt (outre celui d’exister …).

