Question
Bonjour, on me demande de trouver les équations des tangentes au cercle ![]() de centre
de centre ![]() et de rayon 4, qui passent par les points de
et de rayon 4, qui passent par les points de ![]() d’abscisse 3.
d’abscisse 3.
J’ai trouvé les équations suivantes :
![]()
![]()
Pouvez-vous me dire si ma réponse est correcte s’il vous-plaît ? Merci d’avance.
Réponse
Bonsoir,
Votre réponse ressemble beaucoup à la réponse correcte, mais une petite erreur s’est glissée dans votre calcul. On doit normalement trouver :
![]()
![]()
J’emploierai les notations suivantes :
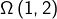 désigne le centre du cercle
désigne le centre du cercle 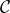
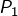 et
et 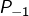 désignent les points de
désignent les points de 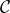 d’abscisse 3 (
d’abscisse 3 (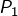 étant celui dont l’ordonnée est la plus grande)
étant celui dont l’ordonnée est la plus grande)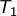 désigne la tangente en
désigne la tangente en 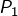 à
à 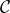
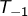 désigne la tangente en
désigne la tangente en 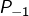 à
à 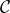
Ces notations peuvent peut-être paraître étranges, mais elles vont permettre d’unifier les calculs (au lieu de faire deux calculs très similaires, l’un avec un signe ‘+’ et l’autre avec un signe ‘-‘).
L’équation cartésienne de ![]() est :
est :
![]()
Pour qu’un point appartienne à ![]() et qu’il soit d’abscisse 3, son ordonnée
et qu’il soit d’abscisse 3, son ordonnée ![]() doit donc vérifier :
doit donc vérifier :
![]()
![]()
![]()
On voit ainsi que :
![Rendered by QuickLaTeX.com \[\boxed{P_{1}\left(\begin{matrix} 3\\ 2+2\sqrt{3}\end{matrix}\right)\qquad P_{-1}\left(\begin{matrix} 3\\ 2-2\sqrt{3}\end{matrix}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-72118470bafd509c1e1b1e77f1bc0401_l3.png)
![]()
A partir de là, je vous propose trois solutions.
Solution 1
Un point ![]() appartient à
appartient à ![]() si, et seulement si, les vecteurs
si, et seulement si, les vecteurs ![]() et
et ![]() sont orthogonaux. Or :
sont orthogonaux. Or :
![]()
On exprime l’orthogonalité de ces deux vecteurs en écrivant que leur produit scalaire est nul :
![]()
![Rendered by QuickLaTeX.com \[\boxed{y=-\frac{\epsilon\sqrt{3}}{3}x+2+3\epsilon\sqrt{3}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e26fb941bc24a6ee07beaa878a5ec7cd_l3.png)
En remplaçant ![]() par 1 ou par -1, on obtient les équations des deux tangentes
par 1 ou par -1, on obtient les équations des deux tangentes ![]() et
et ![]() .
.
Solution 2
Si l’on n’a pas l’habitude du produit scalaire, on peut combiner les propriétés suivantes.
- Etant donnés trois nombres réels
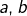 et
et 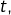 la droite passant par le point de coordonnées
la droite passant par le point de coordonnées 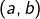 et de pente
et de pente 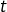 (“ pente ” est synonyme de “ coefficient directeur ”) admet pour équation :
(“ pente ” est synonyme de “ coefficient directeur ”) admet pour équation : 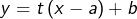 .
. - Deux droites non parallèles à l’axe des ordonnées, de pentes respectives
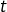 et
et 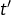 , sont perpendiculaires si, et seulement si
, sont perpendiculaires si, et seulement si 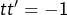 .
.
La droite ![]() a pour pente :
a pour pente :
![]()
La droite ![]() étant perpendiculaire à
étant perpendiculaire à ![]() , sa pente est
, sa pente est ![]() . Comme elle passe par
. Comme elle passe par ![]() , son équation est :
, son équation est :
![]()
On retrouve bien le même résultat que par la première méthode.
Solution 3
Les deux seuls points de ![]() en lesquels la tangente à
en lesquels la tangente à ![]() est horizontale sont ceux de coordonnées
est horizontale sont ceux de coordonnées ![]() et
et ![]() . Ce n’est donc pas le cas des points
. Ce n’est donc pas le cas des points ![]() et
et ![]() .
.
Pour tout ![]() , considérons la droite
, considérons la droite ![]() de pente
de pente ![]() qui passe par
qui passe par ![]() (avec
(avec ![]() donné. Cette droite rencontre évidemment
donné. Cette droite rencontre évidemment ![]() en
en ![]() et, peut-être, en un deuxième point.
et, peut-être, en un deuxième point.
C’est en imposant que ![]() soit le seul point d’intersection que l’on peut exprimer que
soit le seul point d’intersection que l’on peut exprimer que ![]() est une tangente au cercle.
est une tangente au cercle.
Cette droite ![]() admet pour équation :
admet pour équation :
![]()
Il en résulte que l’équation aux abscisses des points d’intersection entre ![]() et
et ![]() est :
est :
![]()
équation qui peut s’écrire :
![]()
et qui se factorise donc sous la forme :
![]()
La condition cherchée est donc :
![]()
ou encore :
![]()
et l’on retrouve (heureusement) le même résultat qu’avec les deux méthodes précédentes.
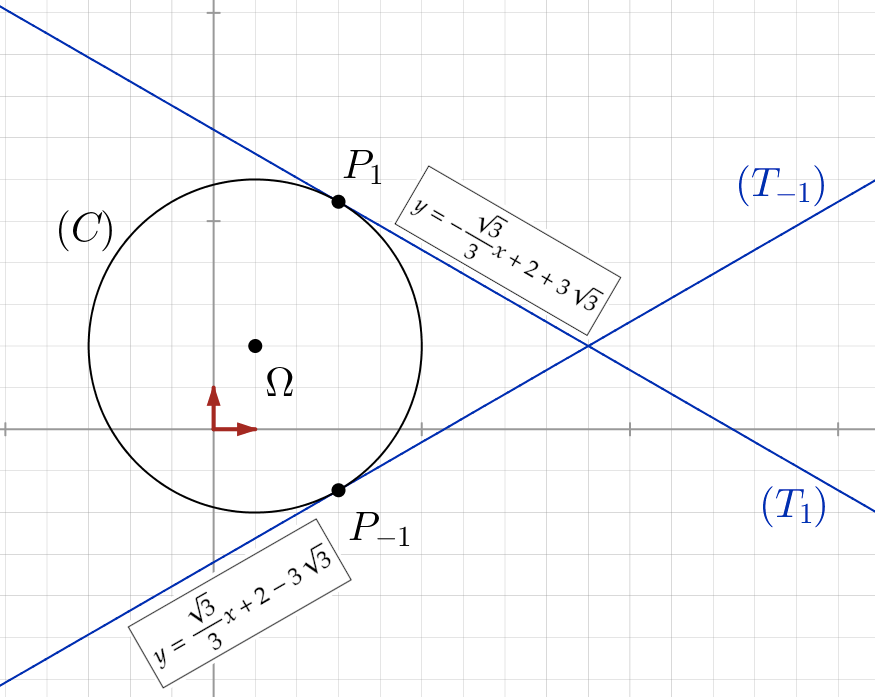
Ci-dessous, une illustration des calculs précédents :