qr-00008

Question

Bonjour je voudrais savoir comment représenter une cotangente dans le cercle trigonométrique. Merci d’avance pour votre réponse.

Réponse

Le schéma ci-dessous représente le cercle trigonométrique \Gamma.

On choisit un point M sur le cercle, de telle sorte qu’une mesure en radians de l’angle \left(\overrightarrow{OA},\overrightarrow{OM}\right) soit \theta\in\left]0,\frac{\pi}{2}\right[.

Par définition :

    \[ \boxed{\tan\left(\theta\right)=\frac{\sin\left(\theta\right)}{\cos\left(\theta\right)}}\]


et

    \[ \boxed{\text{cotan}\left(\theta\right)=\frac{\cos\left(\theta\right)}{\sin\left(\theta\right)}}\]

On note \Delta (resp. \Delta') la droite tangente à \Gamma au point A (resp. B).

La droite \left(OM\right) coupe \Delta en T et \Delta' en T'.

On note encore H (resp. K) le projeté orthogonal de M sur l’axe des abscisses (resp. l’axe des ordonnées).

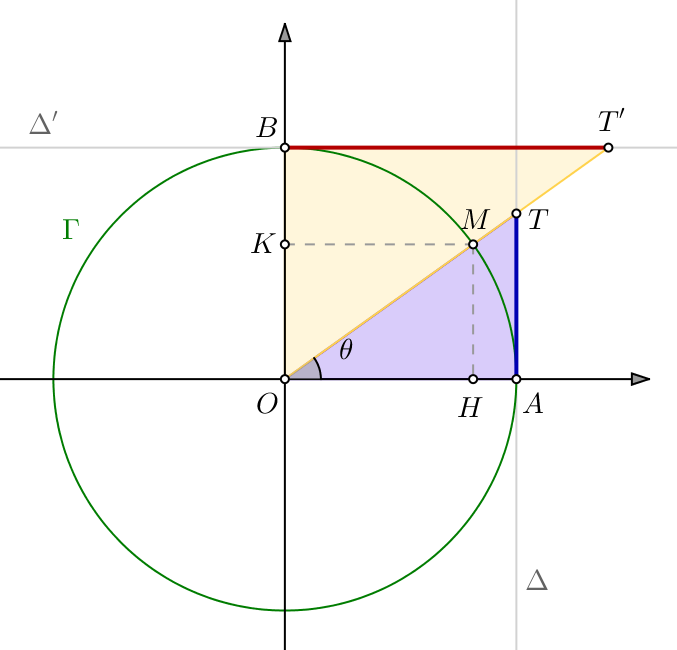
Le théorème de Thalès montre que :

    \[ \frac{\overline{OA}}{\overline{OH}}=\frac{\overline{AT}}{\overline{HM}}=\frac{\overline{AT}}{\overline{OK}}\]


et donc :

    \[ \overline{AT}=\overline{OK}\times\frac{\overline{OA}}{\overline{OH}}=\sin\left(\theta\right)\times\frac{1}{\cos\left(\theta\right)}=\tan\left(\theta\right)\]

On voit de même que :

    \[ \frac{\overline{OB}}{\overline{OK}}=\frac{\overline{BT'}}{\overline{KM}}=\frac{\overline{BT'}}{\overline{OH}}\]


et donc :

    \[ \overline{BT'}=\overline{OH}\times\frac{\overline{OB}}{\overline{OK}}=\cos\left(\theta\right)\times\frac{1}{\sin\left(\theta\right)}=\text{cotan}\left(\theta\right)\]

Bref, la tangente de \theta est matérialisée par la mesure \overline{AT} (qui, on le remarquera, est portée sur une droite … tangente !) et représentée en bleu.

Quant à la cotangente de \theta, elle correspond à la mesure \overline{BT'}, représentée en rouge.

Partager cet article
    

Laisser un commentaire