Lettre G

GÉOMÉTRIQUE (suite, série)

Etant donné un nombre complexe $q,$ on considère la suite de terme général $q^{n}$ (pour $n\in\mathbb{N}).$ Les suites proportionnelles à celle-ci sont dites géométriques de raison $q$ : chaque terme (à partir de celui d’indice 1) est obtenu en multipliant le précédent par $q$ (la raison). Pour une telle suite $\left(u_{n}\right)_{n\geqslant0},$ et pour tout $n\geqslant1$ : $u_{n-1}u_{n+1}=\left(u_{n}\right)^{2}.$ Si les $u_{n}$ sont tous réels positifs, cette relation prend la
forme $u_{n}=\sqrt{u_{n-1}u_{n+1}},$ autrement dit : chaque terme est la moyenne géométrique de ses deux voisins (ce qui montre la cohérence du vocabulaire).

Une CNS pour que la suite $\left(q^{n}\right)_{n\geqslant0}$ soit convergente est $\left|q\right|<1$ (auquel cas la limite est nulle) ou $q=1$ (auquel cas la suite est constante est sa limite est 1).

Si l’on note, pour tout $n\in\mathbb{N}$ :

$S_{n}=\sum_{k=0}^{n}q^{k}$

alors, en supposant $q\neq1$ :

$S_{n}=\frac{1-q^{n+1}}{1-q}$

ce qu’on peut aisément établir par récurrence.

La série $\sum_{n\geqslant0}q^{n}$ est donc convergente lorsque $\left|q\right|<1,$ et sa somme est alors :

$\sum_{n=0}^{\infty}q^{n}=\frac{1}{1-q}$

Pour en savoir plus sur les sommes et les séries géométriques, on pourra consulter cet article.

GRASSMANN (formule de)

En algèbre linéaire, la formule de Grassmann donne la dimension de la somme de deux sous-espaces vectoriels de dimensions finies.

Proposition

Soit $E$ un $\mathbb{K}-$ espace vectoriel et soient $F,G$ deux sous-espaces de dimensions finies. Alors $F+G$ est aussi de dimension finie et :

$\dim\left(F+G\right)=\dim\left(F\right)+\dim\left(G\right)-\dim\left(F\cap G\right)$

Lorsque la somme $F+G$ est directe, cette formule devient :

$\dim\left(F\oplus G\right)=\dim\left(F\right)+\dim\left(G\right)$

Deux preuves de la formule de Grassmann sont disponibles dans cet article. On les trouve précisément ici et là.

Voir aussi cette vidéo et les suivantes pour les questions relatives à la théorie de la dimension.

On notera l’analogie avec deux autres formules :

celle donnant le cardinal de l’union de deux ensembles finis,
celle donnant la probabilité de l’union de deux événements.

Cependant, ces deux dernières formules se généralisent à un nombre (fini) quelconque de termes, alors que la « formule de Grassmann pour trois termes » :

$\begin{eqnarray*}\dim\left(F+G+H\right) & = & \dim\left(F\right)+\dim\left(G\right)+\dim\left(H\right)\\ & & -\left[\dim\left(F\cap G\right)+\dim\left(F\cap H\right)+\dim\left(G\cap H\right)\right]\\ & & +\dim\left(F\cap G\cap H\right)\end{eqnarray*}$

est fausse ! Contre-exemple : ici.

GROUPE

La structure de groupe a été introduite, sous une forme particulière, par Évariste Galois dans le cadre de ses recherches sur les équations algébriques. Elle a été ensuite généralisée et cette généralisation s’est avérée fondamentale dans quasiment tous les secteurs des mathématiques.

Un groupe est un ensemble muni d’une opération associative, possédant un élément neutre et telle que chaque élément admet un symétrique.

L’opération peut être notée par un symbole (comme $+$ , $\times$ ou $\star$ par exemple) ou par simple juxtaposition, moyennant quoi la définition formalisée est la suivante :

Un groupe est un couple $(G,.)$ formé d’un ensemble et d’une opération sur cet ensemble, tels que :

$\forall(a,b,c)\in G^3,\,(ab)c=a(bc)$
$\exists e\in G;\,\forall a\in G,\,ea=ae=a$
$\forall a\in G,\exists b\in G;\,ab=ba=e$

Si l’opération est en outre commutative, c’est-à-dire si :

$\forall (a,b)\in G^2,\,ab=ba$

alors le groupe est dit commutatif (ou abélien, en l’honneur de Niels Henrik Abel).

Des exemples usuels de groupes sont :

le groupe additif des entiers : $\left(\mathbb{Z},+\right)$ ,
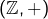le groupe multiplicatif des nombres complexes non nuls : 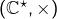$\left(\mathbb{C}^\star,\times\right)$ ,
le $n$ -ème groupe de permutations : 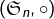$\left(\mathfrak{S}_n,\circ\right)$ ,
le groupe des matrices carrées réelles de taille $n$ , inversibles : $\left(GL_n(\mathbb{R}),\times\right)$ .

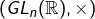On peut citer des exemples plus géométriques, comme le groupe des isométries d’un cube ou encore le groupe des homothéties-translations d’un espace affine.

Partager cet article