Indications pour démarrer les exercices sur les nombres premiers (fiche 02).
Cliquer ici pour accéder aux énoncés.


Penser à l’identité remarquable ![]()
Montrer par l’absurde qu’un tel entier ![]() ne peut pas :
ne peut pas :
- posséder trois facteurs premiers distincts
- être de la forme
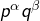 avec
avec 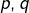 premiers distincts,
premiers distincts, 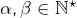 et
et 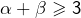
- être de la forme
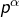 avec
avec 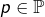 et
et 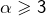

Commencer par écrire une fonction qui calcule le plus petit facteur premier d’un entier ![]() Utiliser la méthode décrite dans cet article.
Utiliser la méthode décrite dans cet article.

Réduire ![]() modulo 3.
modulo 3.

Utiliser l’exercice 8 de la fiche n° 1 sur les nombres premiers.

Examiner les facteurs premiers de l’entier :
![Rendered by QuickLaTeX.com \[A=\left(\prod_{i=1}^{r}p_{i}\right)-1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fe6043be38d89ac647b6ec7b454fd510_l3.png)

Penser au petit théorème de Fermat.
Voir que 2, 3 et 6 sont premiers avec ![]() si
si ![]()

Appliquer la formule de Legendre puis procéder par encadrement.

Il est utile de savoir que tout nombre parfait pair est un nombre d’Euclide , c’est-à-dire de la forme ![]() avec
avec
![]()
