Solutions détaillées de neuf exercices sur les sommes de Riemann (fiche 2)
Cliquer ici pour accéder aux énoncés.
On sait que :
![Rendered by QuickLaTeX.com \[\dfrac{1}{n^{\alpha+1}}\sum_{k=1}^{n}k^{\alpha}=\dfrac{1}{n}\sum_{k=1}^{n}\left(\dfrac{k}{n}\right)^{\alpha}\underset{n\rightarrow+\infty}{\longrightarrow}\int_{0}^{1}t^{\alpha}\thinspace dt=\dfrac{1}{\alpha+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-731dadb218ad42cdcbd6d8dc56a0a2e1_l3.png)
Ainsi, lorsque
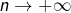
:
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{n}k^{\alpha}\sim\dfrac{n^{\alpha+1}}{\alpha+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7d1fc564ff672cb544cd9ccf405f542d_l3.png)
Après avoir remarqué que, pour tout 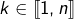 :
:
![Rendered by QuickLaTeX.com \[\dfrac{n+k}{n^{2}+k^{2}}=\dfrac{1}{n}\:\dfrac{1+\frac{k}{n}}{1+\frac{k^{2}}{n^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4d61bcf1c9841bf883b44218ec222310_l3.png)
on somme pour
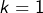
à

et l’on reconnaît une somme de Riemann pour
![Rendered by QuickLaTeX.com f:\left[0,1\right]\rightarrow\mathbb{R},\thinspace t\mapsto\dfrac{1+t}{1+t^{2}}.](https://math-os.com/wp-content/ql-cache/quicklatex.com-87f147fc7d873280ccc2d772e0716a54_l3.png)
Ainsi :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\sum_{k=1}^{n}\dfrac{n+k}{n^{2}+k^{2}}=\int_{0}^{1}\dfrac{1+t}{1+t^{2}}\thinspace dt=\left[\arctan\left(t\right)+\dfrac{1}{2}\ln\left(1+t^{2}\right)\right]_{0}^{1} \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a1bb7bd09a56e573924b9fd0c2900e9d_l3.png)
soit finalement :
![Rendered by QuickLaTeX.com \[ \boxed{\lim_{n\rightarrow+\infty}\sum_{k=1}^{n}\dfrac{n+k}{n^{2}+k^{2}}=\dfrac{\pi}{4}+\dfrac{1}{2}\ln\left(2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c475f8830ce781f7d0a863ccfa6ee075_l3.png)
Posons, pour tout 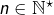 :
:
![Rendered by QuickLaTeX.com \[A_{n}=\sum_{k=1}^{n}\sin\left(\dfrac{k\pi}{n}\right)\qquad\text{et}\qquad G_{n}=\sum_{k=1}^{n}e^{ik\pi/n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-636e8fc0a2de577886c1f51adf11005a_l3.png)
On reconnaît que
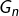
est une somme géométrique de raison
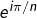
et que
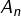
est sa partie imaginaire. Ainsi :
![Rendered by QuickLaTeX.com \[G_{n}=e^{i\pi/n}\thinspace\dfrac{1-e^{i\pi}}{1-e^{i\pi/n}}=\dfrac{2\thinspace e^{i\pi/n}}{1-e^{i\pi/n}}=\dfrac{2\thinspace e^{i\pi/2n}}{-2i\sin\left(\dfrac{\pi}{2n}\right)}=\dfrac{i\thinspace e^{i\pi/2n}}{\sin\left(\dfrac{\pi}{2n}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7c21a75a01fa795a45e554f9436a0c2f_l3.png)
puis :
![Rendered by QuickLaTeX.com \[A_{n}=\cotan\left(\dfrac{\pi}{2n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-abdf66a6e5b4ed47ec66cf948085ee8f_l3.png)
On calcule maintenant, comme demandé, l’intégrale
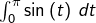
en passant par une somme de Riemann :
![Rendered by QuickLaTeX.com \[\int_{0}^{\pi}\sin\left(t\right)\thinspace dt=\lim_{n\rightarrow+\infty}\dfrac{\pi}{n}\sum_{k=1}^{n}\sin\left(\dfrac{k\pi}{n}\right)=\lim_{n\rightarrow+\infty}\dfrac{\pi}{n}\cotan\left(\dfrac{\pi}{2n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9a17cdd16848ddd794f6141115c06380_l3.png)
c’est-à-dire :
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{\pi}\sin\left(t\right)\thinspace dt=2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2dff3b546374ddfb27bfbde64cccb09a_l3.png)
Remarque
Ce calcul artificiel ne fournit évidemment pas le moyen le plus rapide de calculer cette intégrale ! Il est immédiat que :
![Rendered by QuickLaTeX.com \[\int_{0}^{\pi}\sin\left(t\right)\thinspace dt=\left[-\cos\left(t\right)\right]_{0}^{\pi}=\cos\left(0\right)-\cos\left(\pi\right)=2\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dfac9b42eee9425651c2ffb92ce6d982_l3.png)
Posons, pour tout 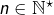 :
:
![Rendered by QuickLaTeX.com \[S_{n}=\frac{b-a}{n}\sum_{k=0}^{n-1}u\left(a+\frac{k\left(b-a\right)}{n}\right)\qquad\text{et}\qquad T_{n}=\frac{b-a}{n}\sum_{k=0}^{n-1}\left(f\circ u\right)\left(a+\frac{k\left(b-a\right)}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9cc0ce3433d3cb043a1a8b919cd204ad_l3.png)
D’après la version discrète de l’inégalité de Jensen :
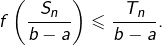
Mais
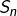
et
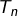
sont des sommes de Riemann, respectivement attachées à

et à
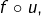
donc en passant à la limite (et vue la continuité de
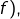
on obtient la conlusion souhaitée, à savoir :
![Rendered by QuickLaTeX.com \[\boxed{f\left(\dfrac{1}{b-a}\int_{a}^{b}\thinspace u\left(t\right)\thinspace dt\right)\leqslant\dfrac{1}{b-a}\int_{a}^{b}f\left(u\left(t\right)\right)\thinspace dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c4d219f185fbc3045fdacac3727681c0_l3.png)
Posons :
![Rendered by QuickLaTeX.com \[F\left(x\right)=\int_{0}^{x}\,f\left(t\right)\,dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d7bc351d36446852fee4fb69fffaf904_l3.png)
Pour tout
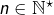
et pour tout
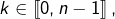
il existe (d’après la formule de Taylor)-Lagrange) un réel
![Rendered by QuickLaTeX.com {\displaystyle c_{n,k}\in\left]\frac{k}{n},\frac{k+1}{n}\right[}](https://math-os.com/wp-content/ql-cache/quicklatex.com-017acbbf2aca80aba281412a959bc417_l3.png)
tel que :
![Rendered by QuickLaTeX.com \[F\left(\frac{k+1}{n}\right)=F\left(\frac{k}{n}\right)+\frac{1}{n}\,f\left(\frac{k}{n}\right)+\frac{1}{2n^{2}}\,f'\left(c_{k,n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0b40a5143934953b7058fb4c2920007b_l3.png)
Par sommation :
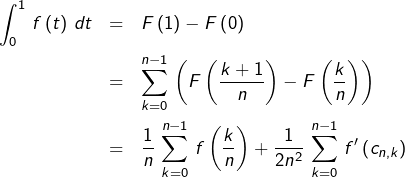
Or
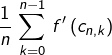
est une somme de Riemann pour
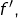
associée à la subdivision pointée
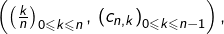
et donc :
![Rendered by QuickLaTeX.com \[ \lim_{n\rightarrow\infty}\,{\displaystyle \frac{1}{n}\,\sum_{k=0}^{n-1}\,f'\left(c_{n,k}\right)}=\int_{0}^{1}\,f'\left(t\right)\,dt=f\left(1\right)-f\left(0\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3346e42d76037250ab3a9b0326730c33_l3.png)
Finalement :
![Rendered by QuickLaTeX.com \[\boxed{\frac{1}{n}\,\sum_{k=0}^{n-1}\,f\left(\frac{k}{n}\right)=\int_{0}^{1}\,f\left(t\right)\,dt-\frac{1}{2n}\,\left(f\left(1\right)-f\left(0\right)\right)+o\left(\frac{1}{n}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-11a0d6c8bb77b90ecfbdc7b499ee7fc9_l3.png)
Posons, pour tout  :
:
![Rendered by QuickLaTeX.com \[A_{n}=\dfrac{1}{n}\sum_{k=1}^{n-1}f\left(\dfrac{k}{n}\right)\thinspace g\left(\dfrac{k+1}{n}\right)\qquad\text{et}\qquad B_{n}=\dfrac{1}{n}\sum_{k=1}^{n-1}f\left(\dfrac{k}{n}\right)\thinspace g\left(\dfrac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-627ec42273d4d871310849b01457fa5e_l3.png)
On sait que :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}B_{n}=\int_{0}^{1}f\left(t\right)\thinspace g\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1f4f2de3fb9e7b09790adcc223ba15ed_l3.png)
Par ailleurs :
![Rendered by QuickLaTeX.com \[\left|A_{n}-B_{n}\right|=\dfrac{1}{n}\left|\sum_{k=1}^{n-1}f\left(\dfrac{k}{n}\right)\left[g\left(\dfrac{k+1}{n}\right)-g\left(\dfrac{k}{n}\right)\right]\right|\leqslant\dfrac{1}{n}\sum_{k=1}^{n-1}\left|f\left(\dfrac{k}{n}\right)\right|\thinspace\left|g\left(\dfrac{k+1}{n}\right)-g\left(\dfrac{k}{n}\right)\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cc68efa27bedba48850c38f87e0d5b50_l3.png)
et donc :
![Rendered by QuickLaTeX.com \[\left|A_{n}-B_{n}\right|\leqslant\dfrac{\left\Vert f\right\Vert_{\infty}}{n}\thinspace\sum_{k=1}^{n-1}\left|g\left(\dfrac{k+1}{n}\right)-g\left(\dfrac{k}{n}\right)\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4548d06d91d71692f2075fffa291540d_l3.png)
Comme
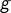
est uniformément continue (d’après le théorème de Heine), étant donné

il existe
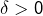
tel que pour tout
![Rendered by QuickLaTeX.com \left(x,x'\right)\in\left[0,1\right]^{2}](https://math-os.com/wp-content/ql-cache/quicklatex.com-6ba6ac1d08118dd25ad32aea24650576_l3.png)
:
![Rendered by QuickLaTeX.com \[\left|x-x'\right|\leqslant\delta\Rightarrow\left|g\left(x\right)-g\left(x'\right)\right|\leqslant\dfrac{\epsilon}{\left\Vert f\right\Vert_{\infty}} \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3ed01ae19ebf283ce2b2087ca80cd32e_l3.png)
En choisissant
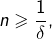
on constate alors que :
![Rendered by QuickLaTeX.com \[ \left|A_{n}-B_{n}\right|\leqslant\dfrac{\left\Vert f\right\Vert_{\infty}}{n}\thinspace\left(n-1\right)\dfrac{\epsilon}{\left\Vert f\right\Vert_{\infty}}\leqslant\epsilon\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ca8583addcb287d3151e8aace077d2f7_l3.png)
Ceci montre que
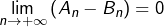
et donc que :
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow+\infty}A_{n}=\int_{0}^{1}f\left(t\right)\thinspace g\left(t\right)\thinspace dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-681c764d1d71a52a5b4ac0cb896b3764_l3.png)
Soit 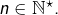 Pour tout
Pour tout 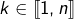 :
:
![Rendered by QuickLaTeX.com \[\dfrac{k}{n}=\left(1-\dfrac{k}{n}\right)\dfrac{k}{n+1}+\dfrac{k}{n}\thinspace\dfrac{k+1}{n+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-78322ce40bd70fdbe2b574a86c537407_l3.png)
donc :
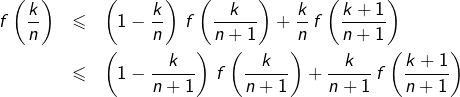
La première inégalité découle de la convexité de
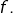
Pour la seconde, on voit que :
![Rendered by QuickLaTeX.com \begin{eqnarray*}& & \left[\left(1-\dfrac{k}{n+1}\right)\thinspace f\left(\dfrac{k}{n+1}\right)+\dfrac{k}{n+1}\thinspace f\left(\dfrac{k+1}{n+1}\right)\right]-\left[\left(1-\dfrac{k}{n}\right)\thinspace f\left(\dfrac{k}{n+1}\right)+\dfrac{k}{n}\thinspace f\left(\dfrac{k+1}{n+1}\right)\right]\\& = & \left(\dfrac{k}{n}-\dfrac{k}{n+1}\right)\left(f\left(\dfrac{k}{n+1}\right)-f\left(\dfrac{k+1}{n+1}\right)\right)\\& \geqslant & 0\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-37e3eca4010201fad851f5b5c69c8660_l3.png)
en raison de la décroissance de
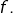
Ensuite, on obtient après sommation :
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}f\left(\dfrac{k}{n}\right)\leqslant\dfrac{1}{n+1}\sum_{k=1}^{n}\left(n+1-k\right)\thinspace f\left(\dfrac{k}{n+1}\right)+\dfrac{1}{n+1}\sum_{k=1}^{n}k\thinspace f\left(\dfrac{k+1}{n+1}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4c56fd421f30e92b05d38eefe1079f2e_l3.png)
On rajoute à cette dernière somme un terme d’indice
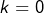
(qui est nul) et on la ré-indexe :
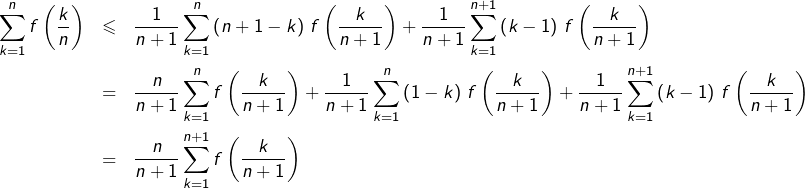
Finalement :
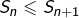
On a prouvé le :
Théorème
Si ![Rendered by QuickLaTeX.com f:\left[0,1\right]\rightarrow\mathbb{R}](https://math-os.com/wp-content/ql-cache/quicklatex.com-24d21c2af9c99ccd14b07bf411b8970d_l3.png) est décroissante et convexe, alors la suite
est décroissante et convexe, alors la suite 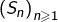 est croissante.
est croissante.
Considérons maintenant :
![Rendered by QuickLaTeX.com \[f:\left[0,1\right]\rightarrow\mathbb{R},\thinspace x\mapsto\left\{ \begin{array}{cc}1 & \text{si }0\leqslant x\leqslant\frac{1}{2}\\0 & \text{sinon}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-40ab66c6be0424fd6db34efcf22e9315_l3.png)
qui est décroissante (au sens large). Alors, pour tout
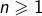
:
![Rendered by QuickLaTeX.com \[S_{n}=\dfrac{1}{n}\left\lfloor \dfrac{n}{2}\right\rfloor\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8289742fcc95457fb3713a1cddb0ea1a_l3.png)
et donc :
![Rendered by QuickLaTeX.com \[\forall p\in\mathbb{N}^{\star},\thinspace\left\{ \begin{array}{ccc}S_{2p-1} & = & \frac{p-1}{2p-1}\\S_{2p} & = & \frac{1}{2}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c1db3e1f262722f6d2be5699ec68e23a_l3.png)
On constate que la suite
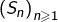
converge vers

en oscillant (en particulier : elle n’est pas croissante).
Intuitivement, lorsque  est grand, tout se passe comme si, sur chacun des segments
est grand, tout se passe comme si, sur chacun des segments ![Rendered by QuickLaTeX.com \left[x_{k,n},\thinspace x_{k+1,n}\right],](https://math-os.com/wp-content/ql-cache/quicklatex.com-dcd83201b293056be2a3680a392df275_l3.png) la fonction
la fonction  « n’avait pas le temps » de changer de signe. Ainsi, lorsque
« n’avait pas le temps » de changer de signe. Ainsi, lorsque  est grand,
est grand, 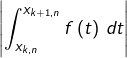 est « le plus souvent » égal à
est « le plus souvent » égal à 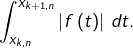 Ceci suggère de montrer que :
Ceci suggère de montrer que :
( )
) ![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}I_{n}=\int_{a}^{b}\left|f\left(t\right)\right|\thinspace dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3a0c35a85b79f58dbc96b8ac8361ad2e_l3.png)
D’après la première formule de la moyenne, pour tout 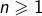 et tout
et tout 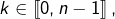 il existe
il existe ![Rendered by QuickLaTeX.com c_{k,n}\in\left[x_{k,n},\thinspace x_{k+1,n}\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1d7d2033dd8cdf0264be00d860fa9859_l3.png) tel que :
tel que :
![Rendered by QuickLaTeX.com \[\int_{x_{k,n}}^{x_{k+1,n}}f\left(t\right)\thinspace dt=\frac{b-a}{n}f\left(c_{k,n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-284a141a73562f8059ab9607ffd60c9b_l3.png)
Introduisons la somme de Riemann :
![Rendered by QuickLaTeX.com \[S_{n}=\frac{b-a}{n}\sum_{k=0}^{n-1}\left|f\left(x_{k,n}\right)\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-caa61283bfe5ce2b39a460d74c2894e2_l3.png)
On sait que :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}S_{n}=\int_{a}^{b}\left|f\left(t\right)\right|\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-460e3adfc7c834c90f3aef9edd1ab765_l3.png)
Pour tout
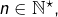
d’après l’inégalité triangulaire :
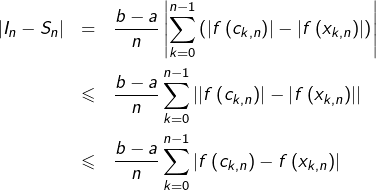
Comme

est uniformément continue (théorème de Heine), il existe pour tout
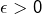
un réel
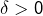
tel que :
![Rendered by QuickLaTeX.com \[\forall\left(t,t'\right)\in\left[a,b\right]^{2},\thinspace\left|t-t'\right|\leqslant\delta\Rightarrow\left|f\left(t\right)-f\left(t'\right)\right|\leqslant\frac{\epsilon}{b-a}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-047241743840a66cafe5a20958ce16f0_l3.png)
Ainsi :
![Rendered by QuickLaTeX.com \[n\geqslant\frac{b-a}{\delta}\Rightarrow\left|I_{n}-S_{n}\right|\leqslant\frac{b-a}{n}\thinspace\frac{n\epsilon}{b-a}=\epsilon\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bb871c1874e8effc8df2f8b86ef87d23_l3.png)
L’égalité

est établie.
Il est connu que l’intégrale 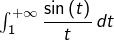 est convergente. En posant
est convergente. En posant 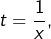 il vient pour tout
il vient pour tout 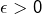 :
:
![Rendered by QuickLaTeX.com \[\int_{\epsilon}^{1}\dfrac{1}{x}\sin\left(\dfrac{1}{x}\right)\thinspace dx=\int_{1}^{1/\epsilon}\thinspace\dfrac{\sin\left(t\right)}{t}\thinspace dt\underset{\epsilon\rightarrow0^{+}}{\longrightarrow}\int_{1}^{+\infty}\dfrac{\sin\left(t\right)}{t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8548e65b95f42352071e833ac48cbf9d_l3.png)
ce qui montre la convergence de l’intégrale
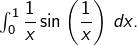
Afin de prouver que la suite 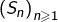 diverge, on prouve que la suite
diverge, on prouve que la suite 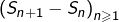 ne converge pas vers
ne converge pas vers 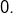 Pour tout
Pour tout 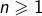 :
:
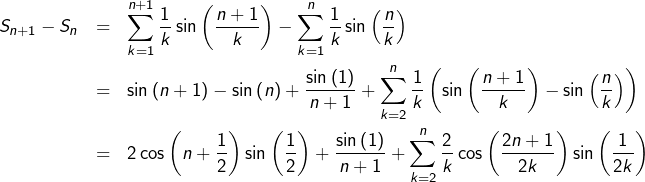
donc :
![Rendered by QuickLaTeX.com \[\left|S_{n+1}-S_{n}-2\cos\left(n+\dfrac{1}{2}\right)\sin\left(\dfrac{1}{2}\right)-\dfrac{\sin\left(1\right)}{n+1}\right|\leqslant\sum_{k=2}^{n}\dfrac{1}{k^{2}}\leqslant\dfrac{\pi^{2}}{6}-1\leqslant0,65\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3cdd7572177a7e511827aece67280a19_l3.png)
et donc :
![Rendered by QuickLaTeX.com \[S_{n+1}-S_{n}-\dfrac{\sin\left(1\right)}{n+1}\geqslant2\cos\left(n+\dfrac{1}{2}\right)\sin\left(\dfrac{1}{2}\right)-0,65\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9d20d27d2bec54806fc87338b8518bb6_l3.png)
Or (cf. détail ci-dessous), il existe une extraction
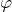
telle que
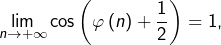
d’où
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}2\cos\left(\varphi\left(n\right)+\dfrac{1}{2}\right)\sin\left(\dfrac{1}{2}\right)-0,65=2\sin\left(\dfrac{1}{2}\right)-0,65>0,3\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f9c24b76352102c6da0df9ef28c3ef70_l3.png)
Ainsi, à partir d’un certain rang :
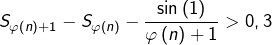
ce qui entraîne que
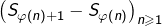
ne converge pas vers
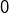
et, a fortiori, que
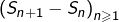
ne converge pas vers
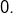
Détail
On sait que 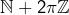 est dense dans
est dense dans 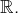 Il existe donc des suites
Il existe donc des suites 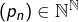 et
et 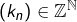 telles que :
telles que :
![Rendered by QuickLaTeX.com \[p_{n}+2\pi k_{n}\rightarrow-\dfrac{1}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-71b6bf1d9dfdffb5c1834af81b185b6c_l3.png)
et donc :
![Rendered by QuickLaTeX.com \[\cos\left(p_{n}+\dfrac{1}{2}\right)\rightarrow1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d6a75a3973c156322da78e4102eba23e_l3.png)
Le lemme des pics dit que, de toute suite réelle, on peut extraire une sous-suite monotone. On peut donc extraire de
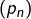
une sous-suite monotone
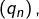
qui n’est pas stationnaire (car il n’existe pas d’entier
tel que
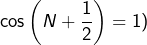
. S’agissant d’une suite d’entiers naturels, cette sous-suite est donc croissante. Elle n’est pas majorée (sans quoi elle serait stationnaire) et admet donc une sous-suite strictement croissante.
Commentaire : l’exemple ci-dessus montre que, sans hypothèse de monotonie, le théorème de convergence des sommes de Riemann pour des intégrales impropres est en défaut (voir l’exercice n° 8 de cette fiche).
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
![Rendered by QuickLaTeX.com \[\dfrac{1}{n^{\alpha+1}}\sum_{k=1}^{n}k^{\alpha}=\dfrac{1}{n}\sum_{k=1}^{n}\left(\dfrac{k}{n}\right)^{\alpha}\underset{n\rightarrow+\infty}{\longrightarrow}\int_{0}^{1}t^{\alpha}\thinspace dt=\dfrac{1}{\alpha+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-731dadb218ad42cdcbd6d8dc56a0a2e1_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{n}k^{\alpha}\sim\dfrac{n^{\alpha+1}}{\alpha+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7d1fc564ff672cb544cd9ccf405f542d_l3.png)
![Rendered by QuickLaTeX.com \[\dfrac{n+k}{n^{2}+k^{2}}=\dfrac{1}{n}\:\dfrac{1+\frac{k}{n}}{1+\frac{k^{2}}{n^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4d61bcf1c9841bf883b44218ec222310_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\sum_{k=1}^{n}\dfrac{n+k}{n^{2}+k^{2}}=\int_{0}^{1}\dfrac{1+t}{1+t^{2}}\thinspace dt=\left[\arctan\left(t\right)+\dfrac{1}{2}\ln\left(1+t^{2}\right)\right]_{0}^{1} \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a1bb7bd09a56e573924b9fd0c2900e9d_l3.png)
![Rendered by QuickLaTeX.com \[ \boxed{\lim_{n\rightarrow+\infty}\sum_{k=1}^{n}\dfrac{n+k}{n^{2}+k^{2}}=\dfrac{\pi}{4}+\dfrac{1}{2}\ln\left(2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c475f8830ce781f7d0a863ccfa6ee075_l3.png)
![Rendered by QuickLaTeX.com \[A_{n}=\sum_{k=1}^{n}\sin\left(\dfrac{k\pi}{n}\right)\qquad\text{et}\qquad G_{n}=\sum_{k=1}^{n}e^{ik\pi/n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-636e8fc0a2de577886c1f51adf11005a_l3.png)
![Rendered by QuickLaTeX.com \[G_{n}=e^{i\pi/n}\thinspace\dfrac{1-e^{i\pi}}{1-e^{i\pi/n}}=\dfrac{2\thinspace e^{i\pi/n}}{1-e^{i\pi/n}}=\dfrac{2\thinspace e^{i\pi/2n}}{-2i\sin\left(\dfrac{\pi}{2n}\right)}=\dfrac{i\thinspace e^{i\pi/2n}}{\sin\left(\dfrac{\pi}{2n}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7c21a75a01fa795a45e554f9436a0c2f_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\int_{0}^{\pi}\sin\left(t\right)\thinspace dt=\lim_{n\rightarrow+\infty}\dfrac{\pi}{n}\sum_{k=1}^{n}\sin\left(\dfrac{k\pi}{n}\right)=\lim_{n\rightarrow+\infty}\dfrac{\pi}{n}\cotan\left(\dfrac{\pi}{2n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9a17cdd16848ddd794f6141115c06380_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{\pi}\sin\left(t\right)\thinspace dt=2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2dff3b546374ddfb27bfbde64cccb09a_l3.png)
![]()
![Rendered by QuickLaTeX.com \[S_{n}=\frac{b-a}{n}\sum_{k=0}^{n-1}u\left(a+\frac{k\left(b-a\right)}{n}\right)\qquad\text{et}\qquad T_{n}=\frac{b-a}{n}\sum_{k=0}^{n-1}\left(f\circ u\right)\left(a+\frac{k\left(b-a\right)}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9cc0ce3433d3cb043a1a8b919cd204ad_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{f\left(\dfrac{1}{b-a}\int_{a}^{b}\thinspace u\left(t\right)\thinspace dt\right)\leqslant\dfrac{1}{b-a}\int_{a}^{b}f\left(u\left(t\right)\right)\thinspace dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c4d219f185fbc3045fdacac3727681c0_l3.png)
![]()
![]()
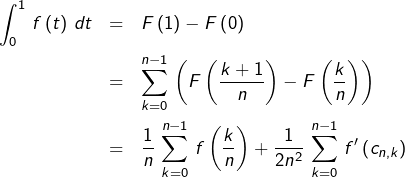
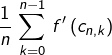 est une somme de Riemann pour
est une somme de Riemann pour ![Rendered by QuickLaTeX.com \[ \lim_{n\rightarrow\infty}\,{\displaystyle \frac{1}{n}\,\sum_{k=0}^{n-1}\,f'\left(c_{n,k}\right)}=\int_{0}^{1}\,f'\left(t\right)\,dt=f\left(1\right)-f\left(0\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3346e42d76037250ab3a9b0326730c33_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\frac{1}{n}\,\sum_{k=0}^{n-1}\,f\left(\frac{k}{n}\right)=\int_{0}^{1}\,f\left(t\right)\,dt-\frac{1}{2n}\,\left(f\left(1\right)-f\left(0\right)\right)+o\left(\frac{1}{n}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-11a0d6c8bb77b90ecfbdc7b499ee7fc9_l3.png)
![Rendered by QuickLaTeX.com \[A_{n}=\dfrac{1}{n}\sum_{k=1}^{n-1}f\left(\dfrac{k}{n}\right)\thinspace g\left(\dfrac{k+1}{n}\right)\qquad\text{et}\qquad B_{n}=\dfrac{1}{n}\sum_{k=1}^{n-1}f\left(\dfrac{k}{n}\right)\thinspace g\left(\dfrac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-627ec42273d4d871310849b01457fa5e_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\left|A_{n}-B_{n}\right|=\dfrac{1}{n}\left|\sum_{k=1}^{n-1}f\left(\dfrac{k}{n}\right)\left[g\left(\dfrac{k+1}{n}\right)-g\left(\dfrac{k}{n}\right)\right]\right|\leqslant\dfrac{1}{n}\sum_{k=1}^{n-1}\left|f\left(\dfrac{k}{n}\right)\right|\thinspace\left|g\left(\dfrac{k+1}{n}\right)-g\left(\dfrac{k}{n}\right)\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cc68efa27bedba48850c38f87e0d5b50_l3.png)
![Rendered by QuickLaTeX.com \[\left|A_{n}-B_{n}\right|\leqslant\dfrac{\left\Vert f\right\Vert_{\infty}}{n}\thinspace\sum_{k=1}^{n-1}\left|g\left(\dfrac{k+1}{n}\right)-g\left(\dfrac{k}{n}\right)\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4548d06d91d71692f2075fffa291540d_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow+\infty}A_{n}=\int_{0}^{1}f\left(t\right)\thinspace g\left(t\right)\thinspace dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-681c764d1d71a52a5b4ac0cb896b3764_l3.png)
![]()
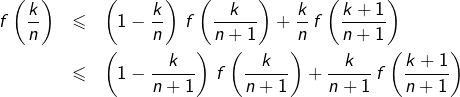
![Rendered by QuickLaTeX.com \begin{eqnarray*}& & \left[\left(1-\dfrac{k}{n+1}\right)\thinspace f\left(\dfrac{k}{n+1}\right)+\dfrac{k}{n+1}\thinspace f\left(\dfrac{k+1}{n+1}\right)\right]-\left[\left(1-\dfrac{k}{n}\right)\thinspace f\left(\dfrac{k}{n+1}\right)+\dfrac{k}{n}\thinspace f\left(\dfrac{k+1}{n+1}\right)\right]\\& = & \left(\dfrac{k}{n}-\dfrac{k}{n+1}\right)\left(f\left(\dfrac{k}{n+1}\right)-f\left(\dfrac{k+1}{n+1}\right)\right)\\& \geqslant & 0\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-37e3eca4010201fad851f5b5c69c8660_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}f\left(\dfrac{k}{n}\right)\leqslant\dfrac{1}{n+1}\sum_{k=1}^{n}\left(n+1-k\right)\thinspace f\left(\dfrac{k}{n+1}\right)+\dfrac{1}{n+1}\sum_{k=1}^{n}k\thinspace f\left(\dfrac{k+1}{n+1}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4c56fd421f30e92b05d38eefe1079f2e_l3.png)
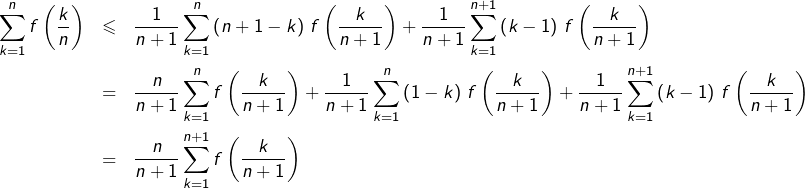
![]()
![]()
![Rendered by QuickLaTeX.com \[\forall p\in\mathbb{N}^{\star},\thinspace\left\{ \begin{array}{ccc}S_{2p-1} & = & \frac{p-1}{2p-1}\\S_{2p} & = & \frac{1}{2}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c1db3e1f262722f6d2be5699ec68e23a_l3.png)
![]() )
) ![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}I_{n}=\int_{a}^{b}\left|f\left(t\right)\right|\thinspace dt}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3a0c35a85b79f58dbc96b8ac8361ad2e_l3.png)
![]()
![Rendered by QuickLaTeX.com \[S_{n}=\frac{b-a}{n}\sum_{k=0}^{n-1}\left|f\left(x_{k,n}\right)\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-caa61283bfe5ce2b39a460d74c2894e2_l3.png)
![]()
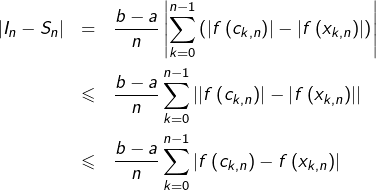
![]()
![]()
![]()
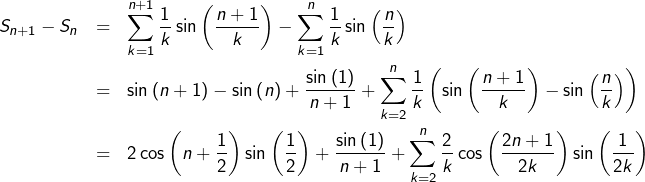
![Rendered by QuickLaTeX.com \[\left|S_{n+1}-S_{n}-2\cos\left(n+\dfrac{1}{2}\right)\sin\left(\dfrac{1}{2}\right)-\dfrac{\sin\left(1\right)}{n+1}\right|\leqslant\sum_{k=2}^{n}\dfrac{1}{k^{2}}\leqslant\dfrac{\pi^{2}}{6}-1\leqslant0,65\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3cdd7572177a7e511827aece67280a19_l3.png)
![]()
![]()
![]()
![]()








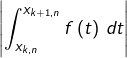 est « le plus souvent » égal à
est « le plus souvent » égal à 