Solutions détaillées de neuf exercices sur le second degré (fiche 01).
Cliquer ici pour accéder aux solutions.


L’erreur consiste à écrire que le carré de ![]() serait
serait
![]()
Il s’agit en fait de ![]() c’est-à-dire
c’est-à-dire
![]()

Il s’agit ici d’une erreur de signe. Voici le calcul correct :
![]()

On ne peut simplifier par ![]() que si
que si ![]() . Voici à présent une résolution correcte.
. Voici à présent une résolution correcte.
L’équation ![]() équivaut à
équivaut à ![]() , c’est-à-dire
, c’est-à-dire ![]() . Or on sait qu’un produit de facteurs (réels) est nul si, et seulement si, l’un au moins des facteurs est nul. Par conséquent l’équation proposée équivaut à :
. Or on sait qu’un produit de facteurs (réels) est nul si, et seulement si, l’un au moins des facteurs est nul. Par conséquent l’équation proposée équivaut à : ![]() ou
ou ![]() .
.
- Pour l’équation
on procède exactement comme à l’exercice précédent. Les solutions sont 0 et 4.![Rendered by QuickLaTeX.com \[\boxed{x^2-4x=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-528c30de2271c449c213bbd0a4f8c10e_l3.png)
- Pour
on regroupe tous les termes dans un membre, ce qui donne l’équation équivalente![Rendered by QuickLaTeX.com \[\boxed{10x-x^2=5x^2+x}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0580809b153e18e423600f7dec1cd5b2_l3.png)
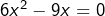 , ou encore (après factorisation par
, ou encore (après factorisation par  ) :
) : 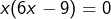 . Finalement, on trouve deux solutions :
. Finalement, on trouve deux solutions : 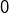 et
et 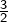 .
. - L’équation
équivaut à![Rendered by QuickLaTeX.com \[\boxed{x^2-1=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3ec2fc476114a1d7ea9e15b66e9a61a0_l3.png)
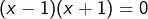 et ses solutions sont -1 et 1.
et ses solutions sont -1 et 1. - Même chose pour l’équation
qui s’écrit![Rendered by QuickLaTeX.com \[\boxed{(x+1)^2=9}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1069a87ff56e33fa9f19c42e53b47636_l3.png)
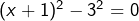 , donc se factorise en
, donc se factorise en 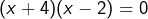 . Ses solutions sont -4 et 2.
. Ses solutions sont -4 et 2. - De même pour
On a une différence de deux carrés qui est nulle. Après factorisation, on aboutit à l’équation équivalente![Rendered by QuickLaTeX.com \[\boxed{(2x+3)^2=(x-4)^2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b9097605ef32d7985fdbf4e90125e0d9_l3.png)
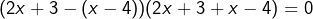 , c’est-à-dire
, c’est-à-dire 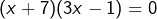 . Les solutions sont -7 et
. Les solutions sont -7 et 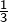 .
. - Enfin l’équation
n’a pas de solution réelle puisque, pour tout![Rendered by QuickLaTeX.com \[\boxed{7x^2+1=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9aac74ce300f0aa55d49d68169501e72_l3.png)
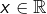 :
: 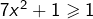 .
.
- L’équation
s’écrit aussi![Rendered by QuickLaTeX.com \[\boxed{x^2+2x+1=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0c3cfd772e142b7c384246118c782f86_l3.png)
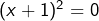 et sa seule solution est -1.
et sa seule solution est -1. - L’équation
équivaut à![Rendered by QuickLaTeX.com \[\boxed{6x-x^2=9}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e589ab7aa035612c6ef744093a676cc8_l3.png)
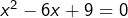 , c’est-à-dire
, c’est-à-dire 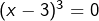 . L’unique solution est 3.
. L’unique solution est 3. - L’équation
équivaut à![Rendered by QuickLaTeX.com \[\boxed{4x^2+4x=1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a5646a926428178d534409f219f532b5_l3.png)
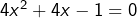 , c’est-à-dire
, c’est-à-dire 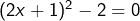 . On factorise, ce qui donne l’équation équivalente
. On factorise, ce qui donne l’équation équivalente 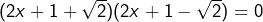 . Les solutions sont donc
. Les solutions sont donc 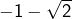 et
et 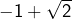 .
. - Pour l’équation
il serait maladroit de développer ! On factorise plutôt par![Rendered by QuickLaTeX.com \[\boxed{5x(x+1)=(x+1)(x+2)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fcd2b979a87f795177e8706827c29fff_l3.png)
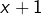 , ce qui donne l’équation équivalente
, ce qui donne l’équation équivalente 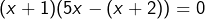 , c’est-à-dire
, c’est-à-dire 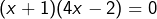 . Les solutions sont donc -1 et
. Les solutions sont donc -1 et 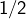 .
. - On passe à l’équation
Après développement et regroupement des termes dans un seul membre, on trouve l’équation équivalente![Rendered by QuickLaTeX.com \[\boxed{(x+3)^2+(x-3)^2=12x}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-da91b1beb5001d46d02c955827606aa5_l3.png)
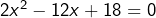 , c’est-à-dire
, c’est-à-dire 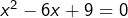 . On met cette dernière sous la forme
. On met cette dernière sous la forme 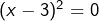 et il apparaît que 3 est la seule solution.
et il apparaît que 3 est la seule solution. - Enfin, la dernière équation s’écrit (après simplification par 2) :
c’est-à-dire![Rendered by QuickLaTeX.com \[\boxed{9x^2-24x+16=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0e57f136f1fdfd0fdfc84ee6c9d5c29c_l3.png)
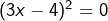 . Sa seule solution est donc
. Sa seule solution est donc 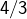 .
.
- L’équation
équivaut à![Rendered by QuickLaTeX.com \[\boxed{x^2+2x-3=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-14230f1e1e8d627789b4a326b43c2674_l3.png)
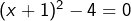 et se factorise sous la forme
et se factorise sous la forme 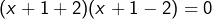 , c’est-à-dire
, c’est-à-dire 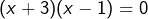 . Ses solutions sont donc -3 et 1.
. Ses solutions sont donc -3 et 1. - L’équation
peut se mettre sous la forme![Rendered by QuickLaTeX.com \[\boxed{4x^2+x+1=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2f65dff777d143299c7e54b9e8e530d4_l3.png)
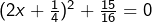 , dont le membre de gauche ne peut s’annuler (il est, pour tout
, dont le membre de gauche ne peut s’annuler (il est, pour tout  réel, minoré par
réel, minoré par 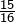 ). Il n’y a donc aucune solution.
). Il n’y a donc aucune solution. - On transforme l’équation
en divisant chaque membre par![Rendered by QuickLaTeX.com \[\boxed{2x^2-5x+2=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4978357107eec03202f1b84bb0811ef0_l3.png)
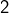 , puis en faisant apparaître un carré. Elle équivaut ainsi à
, puis en faisant apparaître un carré. Elle équivaut ainsi à 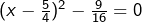 , qui se factorise pour donner
, qui se factorise pour donner 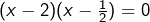 . Les solutions sont donc
. Les solutions sont donc 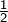 et 2.
et 2. - Pour l’équation
on développe et on regroupe, pour obtenir l’équation équivalente![Rendered by QuickLaTeX.com \[\boxed{(x-2)^2=x}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-530792fc992e566e8674d132e2d482e7_l3.png)
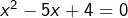 , qui peut s’écrire
, qui peut s’écrire 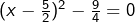 , c’est-à-dire
, c’est-à-dire 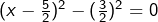 . On factorise et on obtient l’équation équivalente
. On factorise et on obtient l’équation équivalente 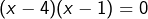 . Les solutions sont donc 1 et 4.
. Les solutions sont donc 1 et 4. - On transforme l’équation
en développant le membre de droite puis en regroupant les termes dans un seul membre. Il vient![Rendered by QuickLaTeX.com \[\boxed{3x^2-1=4(x+\frac12)^2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4702300bfcd716ac028d82891c4da8f7_l3.png)
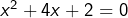 , que l’on met sous la forme
, que l’on met sous la forme 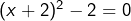 . On factorise pour obtenir l’équation équivalente
. On factorise pour obtenir l’équation équivalente 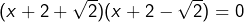 . Les solutions sont
. Les solutions sont 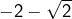 et
et 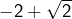 .
. - Même méthode pour l’équation
ce qui donne l’équation équivalente![Rendered by QuickLaTeX.com \[\boxed{(x+1)^2+(x+2)^2=x+3}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0c477ae641e2c262e03acea92aca98b6_l3.png)
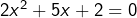 , ou encore
, ou encore 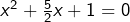 . On met sous forme canonique :
. On met sous forme canonique : 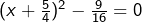 . Les solutions sont -2 et
. Les solutions sont -2 et 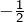 .
.
Accélérons le tempo, puisque c’est toujours la même chose … - Pour
les solutions sont -1 et![Rendered by QuickLaTeX.com \[\boxed{3x^2+2x-1=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6ab1dc30e02a4347e896fee1486aae3d_l3.png)
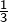 .
. - Pour
les solutions sont![Rendered by QuickLaTeX.com \[\boxed{7x^2+6x=2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-01959659b728533a26fd88a77fa87f84_l3.png)
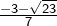 et
et 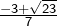 .
. - Pour
les solutions sont![Rendered by QuickLaTeX.com \[\boxed{\frac{x^2}7+\frac x6-\frac15=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2229e564ff1c8559dc16e1633d965451_l3.png)
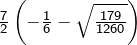 et
et 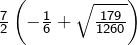

- Pour l’équation
on cherche les solutions dans![Rendered by QuickLaTeX.com \[\boxed{\frac 1x+\frac 1{x+1}=\frac 1{x+3}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e274e9a336ad3552808f898a00dfe982_l3.png)
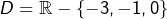 . En regroupant tous les termes dans un membre et après réduction au même dénominateur (qui est
. En regroupant tous les termes dans un membre et après réduction au même dénominateur (qui est 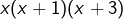 ), l’équation équivaut à
), l’équation équivaut à 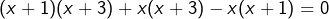 , c’est-à-dire
, c’est-à-dire 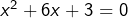 . Le solutions de cette dernière sont
. Le solutions de cette dernière sont 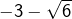 et
et 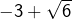 (et elles sont retenues puisqu’elles appartiennent à
(et elles sont retenues puisqu’elles appartiennent à 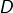 ).
). - L’équation
n’est définie que pour![Rendered by QuickLaTeX.com \[\boxed{\frac x{2+\frac 1{x-1}}=1-x}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-74197662d41b1891ed41648315c1d12e_l3.png)
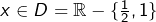 . Pour un tel
. Pour un tel  , elle équivaut à
, elle équivaut à 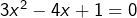 . Le solutions de cette dernière équation du second degré sont
. Le solutions de cette dernière équation du second degré sont 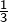 et 1, mais 1 est à rejeter. Finalement : une seule solution :
et 1, mais 1 est à rejeter. Finalement : une seule solution : 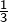 .
. - Pour résoudre l’équation
on dispose essentiellement de deux méthodes. La première consiste à distinguer deux cas selon le signe de![Rendered by QuickLaTeX.com \[\boxed{x^2-5\vert x\vert+6=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-14d110f9ff25c9764ba99e9ff4749e27_l3.png)
 : on est ainsi conduit à résoudre l’équation
: on est ainsi conduit à résoudre l’équation 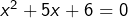 dans
dans ![Rendered by QuickLaTeX.com ]-\infty,0]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9732ee16fdc01c8788aecf8a29adbd4c_l3.png) , l’équation
, l’équation 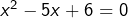 dans
dans 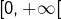 et à réunir les deux ensembles partiels de solutions. La seconde méthode consiste à changer d’inconnue en posant
et à réunir les deux ensembles partiels de solutions. La seconde méthode consiste à changer d’inconnue en posant 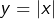 . L’équation transformée
. L’équation transformée 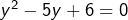 possède deux solutions, à savoir
possède deux solutions, à savoir 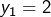 et
et 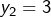 . On résout alors chacune des équations
. On résout alors chacune des équations 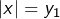 et
et 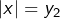 et l’on réunit, là encore, les ensembles de solutions obtenus. D’une manière ou d’une autre, l’équation proposée possède quatre solutions : -3, -2, 2 et 3.
et l’on réunit, là encore, les ensembles de solutions obtenus. D’une manière ou d’une autre, l’équation proposée possède quatre solutions : -3, -2, 2 et 3. - Pour l’équation
on peut factoriser et obtenir l’équation équivalente![Rendered by QuickLaTeX.com \[\boxed{(x^2-1)^2=9}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-007c1ae73a6c0341c53533cb59d413e5_l3.png)
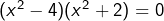 . Comme la condition
. Comme la condition 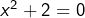 n’est vérifiée pour aucun réel
n’est vérifiée pour aucun réel  , on parvient à deux solutions seulement : -2 et 2.
, on parvient à deux solutions seulement : -2 et 2. - L’équation
n’est définie que pour![Rendered by QuickLaTeX.com \[\boxed{5x-7\sqrt x-12=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b7a193ea4301bab765157d084e578233_l3.png)
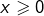 . En posant
. En posant 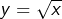 , l’équation transformée est
, l’équation transformée est 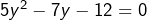 , dont les solutions sont
, dont les solutions sont 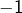 et
et 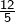 . La première est exclue (car une racine carrée est positive ou nulle). En résolvant
. La première est exclue (car une racine carrée est positive ou nulle). En résolvant 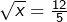 , on trouve l’unique solution :
, on trouve l’unique solution : 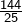
- Enfin, on traite l’équation
en posant![Rendered by QuickLaTeX.com \[\boxed{x^6-16x^3+64=0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-da7af7d3dbb46cbe4518e5fe24540603_l3.png)
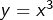 , ce qui nous amène à l’équation transformée (du second degré en
, ce qui nous amène à l’équation transformée (du second degré en 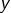 ) :
) : 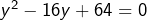 , dont l’unique solution est
, dont l’unique solution est 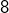 . On doit alors résoudre
. On doit alors résoudre 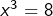 , qui équivaut à
, qui équivaut à 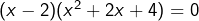 et possède donc 2 pour seule solution.
et possède donc 2 pour seule solution.
➡ Si ![]() , il s’agit d’une équation du premier degré :
, il s’agit d’une équation du premier degré : ![]() . Celle-ci possède
. Celle-ci possède ![]() pour seule solution.
pour seule solution.
➡ Si ![]() , l’équation proposée est du second degré et une CNS (condition nécessaire et suffisante) pour qu’elle possède une solution unique est que son discriminant
, l’équation proposée est du second degré et une CNS (condition nécessaire et suffisante) pour qu’elle possède une solution unique est que son discriminant
![]()
![]()
![]()
Par hypothèse :
![]()
![]()
![]()
![]()
Il est clair que :
![]()
![]()
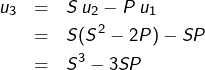
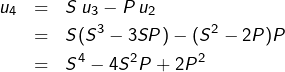
Remarque
Si de plus ![]() et si
et si ![]() sont des entiers (vérifiant donc
sont des entiers (vérifiant donc ![]() ), alors
), alors ![]() sont aussi des entiers et la formule
sont aussi des entiers et la formule ![]() montre (par une récurrence immédiate) que :
montre (par une récurrence immédiate) que :
![]()
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
