Solutions détaillées de neuf exercices sur le raisonnement par récurrence (fiche 02).
Cliquer ici pour accéder aux énoncés.


Quelques essais conduisent à conjecturer que :
![Rendered by QuickLaTeX.com \[\boxed{\forall n\in\mathbb{N}^{\star},\thinspace\forall x\geqslant0,\thinspace f^{n}\left(x\right)=\frac{F_{n}+F_{n-1}x}{F_{n+1}+F_{n}x}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2ee8d8145e3cbc98bd0b13092b7d11e5_l3.png)
![]()
![]()
Alors, pour tout ![]() :
:
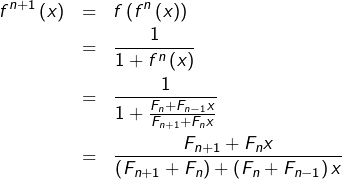
c’est-à-dire, comme souhaité :
![]()

Le réel ![]() étant fixé, on observe que cette inégalité est évidente pour
étant fixé, on observe que cette inégalité est évidente pour ![]() et pour
et pour ![]()
Supposons-la vraie aux rangs ![]() et
et ![]() pour un certain
pour un certain ![]() Comme :
Comme :
![]()
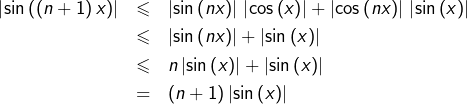

On commence par calculer ![]() pour de petites valeurs de
pour de petites valeurs de ![]() :
:
![]()
![]()
![]()
Montrons par récurrence que ![]() pour tout
pour tout ![]() L’initialisation étant (largement) faite, passons à l’hérédité.
L’initialisation étant (largement) faite, passons à l’hérédité.
On suppose donc l’égalité établie au rang ![]()
L’ensemble des parties non vides de ![]() est l’union disjointe de l’ensemble des parties non vides de
est l’union disjointe de l’ensemble des parties non vides de ![]() et de l’ensemble des parties de
et de l’ensemble des parties de ![]() qui contiennent
qui contiennent ![]()
De plus les parties de ![]() qui contiennent
qui contiennent ![]() sont exactement les
sont exactement les ![]() où
où ![]() parcourt
parcourt ![]() Donc :
Donc :
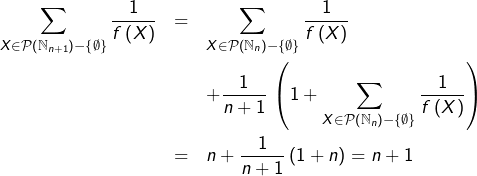

Calculons de deux façons la somme :
![Rendered by QuickLaTeX.com \[\Delta\left(n,p\right)=\sum_{k=1}^{n}\left(\left(k+1\right)^{p+1}-k^{p+1}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d9acbb5f36cf237b6047c3b07d37e2fd_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\left(k+1\right)^{p+1}=\sum_{j=0}^{p+1}\binom{p+1}{j}k^{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dc6af1b496cf1cff6c16596c88d8f2e9_l3.png)
![Rendered by QuickLaTeX.com \[\left(k+1\right)^{p+1}-k^{p+1}=\sum_{j=0}^{p}\binom{p+1}{j}k^{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9bcba625629816fe0a4e80dda34708b3_l3.png)
![Rendered by QuickLaTeX.com \[\Delta\left(n,p\right)=\sum_{k=1}^{n}\sum_{j=0}^{p}\binom{p+1}{j}k^{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-10a6e52333e87555a9450360f3b9e3d4_l3.png)
![Rendered by QuickLaTeX.com \[\Delta\left(n,p\right)=\sum_{j=0}^{p}\sum_{k=1}^{n}\binom{p+1}{j}k^{j}=\sum_{j=0}^{p}\binom{p+1}{j}S_{j}\left(n\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e80cd33c21e835cf02e9a7279860da2f_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\sum_{j=0}^{p}\binom{p+1}{j}S_{j}\left(n\right)=\left(n+1\right)^{p+1}-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d3c88879c8286b574fd7efdd5c28c92d_l3.png)
![Rendered by QuickLaTeX.com \[S_{p}\left(n\right)=\frac{1}{p+1}\left[\left(n+1\right)^{p+1}-1-\sum_{j=0}^{p-1}\binom{p+1}{j}S_{j}\left(n\right)\right]\qquad\left(\star\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0d27cff7be1c7af4478300031ac91164_l3.png)
Supposons établi que, pour un certain ![]() et pour chaque
et pour chaque ![]()
![]() est polynomiale de degré
est polynomiale de degré ![]() La formule
La formule ![]() montre alors que
montre alors que ![]() est polynomiale de degré
est polynomiale de degré ![]() (en effet, l’expression
(en effet, l’expression ![]() est de degré
est de degré ![]() en
en ![]() et la somme qui suit à l’intérieur du crochet est une combinaison linéaire d’expressions polynomiales de degrés
et la somme qui suit à l’intérieur du crochet est une combinaison linéaire d’expressions polynomiales de degrés ![]()
Enfin, l’unicité de ![]() résulte du fait que deux fonctions polynomiales qui coïncident sur un ensemble infini (ici :
résulte du fait que deux fonctions polynomiales qui coïncident sur un ensemble infini (ici : ![]() sont identiques.
sont identiques.

Notons ![]() l’assertion :
l’assertion :
![Rendered by QuickLaTeX.com \[\boxed{\forall\left(x_{1},\cdots,x_{n}\right)\in\mathbb{R}^{n},\thinspace\forall\left(y_{1},\cdots,y_{n}\right)\in\mathbb{R}^{n},\thinspace\left(\sum_{i=1}^{n}x_{i}y_{i}\right)^{2}\leqslant\left(\sum_{i=1}^{n}x_{i}^{2}\right)\left(\sum_{i=1}^{n}y_{i}^{2}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-baa9510b49d4f0ad2a29fdda637372e0_l3.png)
Supposons ![]() vraie pour un certain entier
vraie pour un certain entier ![]() et soient alors
et soient alors ![]()
D’une part :
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left(\sum_{i=1}^{n+1}a_{i}b_{i}\right)^{2} & = & \left[\left(\sum_{i=1}^{n}a_{i}b_{i}\right)+a_{n+1}b_{n+1}\right]^{2}\\& = & \left(\sum_{i=1}^{n}a_{i}b_{i}\right)^{2}+2a_{n+1}b_{n+1}\left(\sum_{i=1}^{n}a_{i}b_{i}\right)+a_{n+1}^{2}b_{n+1}^{2}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-7a6bf6f0eaeaee387d9a08391774d0f9_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left(\sum_{i=1}^{n+1}\,a_{i}^{2}\right)\left(\sum_{i=1}^{n+1}\,b_{i}^{2}\right) & = & \left[\left(\sum_{i=1}^{n}\,a_{i}^{2}\right)+a_{n+1}^{2}\right]\left[\left(\sum_{i=1}^{n}\,b_{i}^{2}\right)+b_{n+1}^{2}\right]\\& = & \left(\sum_{i=1}^{n}\,a_{i}^{2}\right)\left(\sum_{i=1}^{n}\,b_{i}^{2}\right)+a_{n+1}^{2}\left(\sum_{i=1}^{n}\,b_{i}^{2}\right)+b_{n+1}^{2}\left(\sum_{i=1}^{n}\,a_{i}^{2}\right)+a_{n+1}^{2}b_{n+1}^{2}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-0410f0d33c2e19bfbbf9c833ce7a5161_l3.png)
![Rendered by QuickLaTeX.com \[a_{n+1}^{2}\left(\sum_{i=1}^{n}\,b_{i}^{2}\right)+b_{n+1}^{2}\left(\sum_{i=1}^{n}\,a_{i}^{2}\right)-2a_{n+1}b_{n+1}\left(\sum_{i=1}^{n}a_{i}b_{i}\right)\geqslant0\qquad\left(\spadesuit\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a9ccc215359f4bc11dbdbff398fb1e56_l3.png)
![]()

Pour ![]() c’est la définition de la convexité.
c’est la définition de la convexité.
Supposons le résultat établi pour un certain ![]() et soient alors
et soient alors ![]() ainsi que
ainsi que ![]() tels que
tels que 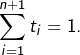 Posons :
Posons :
![Rendered by QuickLaTeX.com \[T=\sum_{i=1}^{n}t_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-53ecbab150435e39d58da6dafcc5867f_l3.png)
En supposant ![]() on observe que :
on observe que :
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{n+1}t_{i}x_{i}=T\left(\sum_{i=1}^{n}\frac{t_{i}}{T}x_{i}\right)+\left(1-T\right)x_{n+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d2c202b97d1c26f30005dc278a41b4da_l3.png)
![Rendered by QuickLaTeX.com \[f\left(\sum_{i=1}^{n+1}t_{i}x_{i}\right)\leqslant T\thinspace f\left(\sum_{i=1}^{n}\frac{t_{i}}{T}x_{i}\right)+\left(1-T\right)\thinspace f\left(x_{n+1}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0eaf3878263bda2bd4ad635ede399497_l3.png)
![Rendered by QuickLaTeX.com \[f\left(\sum_{i=1}^{n+1}t_{i}x_{i}\right)\leqslant T\thinspace\sum_{i=1}^{n}\frac{t_{i}}{T}f\left(x_{i}\right)+\left(1-T\right)\thinspace f\left(x_{n+1}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-43f565b776588dd4efcc5c1f7a25b9c8_l3.png)
![Rendered by QuickLaTeX.com \[f\left(\sum_{i=1}^{n+1}t_{i}x_{i}\right)\leqslant\sum_{i=1}^{n+1}t_{i}\thinspace f\left(x_{i}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a44688b3e245c2e718467435bdc274ff_l3.png)

Soit ![]() Montrons que l’assertion suivante est vraie pour tout entier
Montrons que l’assertion suivante est vraie pour tout entier ![]() :
:
Assertion 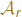
Quels que soient les vecteurs propres ![]() (pour
(pour ![]() associés à des valeurs propres
associés à des valeurs propres ![]() toutes distinctes, la famille
toutes distinctes, la famille ![]() est libre.
est libre.
Pour ![]() aucun problème puisqu’une famille réduite à un seul vecteur non nul est libre.
aucun problème puisqu’une famille réduite à un seul vecteur non nul est libre.
Supposons le résultat établi au rang ![]() pour un certain
pour un certain ![]()
Soient alors ![]() des valeurs propres de
des valeurs propres de ![]() deux à deux distinctes et soient
deux à deux distinctes et soient ![]() des vecteurs propres respectivement associés aux
des vecteurs propres respectivement associés aux ![]()
Considérons des scalaires ![]() tels que :
tels que :
(1) ![Rendered by QuickLaTeX.com \[\sum_{i=1}^{r+1}\alpha_{i}x_{i}=0_{E}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8eee8d85ae5fa19e1e3de528e23bf4ff_l3.png)
(2) ![Rendered by QuickLaTeX.com \[\sum_{i=1}^{r+1}\alpha_{i}\lambda_{i}x_{i}=0_{E}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5522fbc13f2d2295f58996a9736443d9_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{r}\alpha_{i}\left(\lambda_{i}-\lambda_{r+1}\right)x_{i}=0_{E}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e72359b6d1d3d68ffe517ac4b0ea9e08_l3.png)
![]()
Ceci impose ![]() pour tout
pour tout ![]()
Enfin, en reportant dans (1) et compte tenu de ![]() on obtient
on obtient ![]()
La famille ![]() est donc libre, comme souhaité.
est donc libre, comme souhaité.

Montrons par récurrence que l’assertion ![]() suivante est vraie pour tout
suivante est vraie pour tout ![]() :
:
Pour toute famille ![]() si les vecteurs
si les vecteurs ![]() sont tous combinaisons linéaires de
sont tous combinaisons linéaires de ![]() alors la famille
alors la famille ![]() est liée.
est liée.
Pour ![]() c’est simple : si
c’est simple : si ![]() et
et ![]() alors
alors ![]() est liée. En effet, c’est évident
est liée. En effet, c’est évident
si ![]() et sinon, cela résulte de
et sinon, cela résulte de ![]()
Supposons la propriété établie au rang ![]() et soient alors
et soient alors ![]() des vecteurs de
des vecteurs de ![]() et
et ![]() des combinaisons linéaires des
des combinaisons linéaires des ![]() On dispose pour chaque
On dispose pour chaque ![]() d’une expression de
d’une expression de ![]() de la forme :
de la forme :
![Rendered by QuickLaTeX.com \[y_{i}=\sum_{j=1}^{n+1}\,\lambda_{i,j}\,x_{j}\qquad\qquad\left(\blacksquare_{i}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-01d416e9a8571e6385bab67b89446887_l3.png)
Si
Sinon, ![]()
Quitte à ré-indexer, on peut supposer pour simplifier que ![]() Il vient alors, d’après
Il vient alors, d’après ![]() :
:
![Rendered by QuickLaTeX.com \[x_{n+1}=\frac{1}{\lambda_{1,n+1}}\left(y_{1}-\sum_{j=1}^{n}\,\lambda_{1,j}\,x_{j}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f2f99ee23470def5d2d35dde686f3253_l3.png)
D’où, en remplaçant dans
![Rendered by QuickLaTeX.com \[y_{i}=\sum_{j=1}^{n}\,\lambda_{i,j}\,x_{j}+\frac{\lambda_{i,n+1}}{\lambda_{1,n+1}}\left(y_{1}-\sum_{j=1}^{n}\,\lambda_{1,j}\,x_{j}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-eeaada5a50b86bacf33bf85359c4b75e_l3.png)
Par conséquent, en posant :
![]()
on constate que
![Rendered by QuickLaTeX.com \[\exists\left(\mu_{2},\cdots,\mu_{n+2}\right)\in\mathbb{\mathbb{K}}^{n+1}-\left\{ \left(0,\cdots,0\right)\right\} ;\,\sum_{i=2}^{n+2}\,\mu_{i}\,z_{i}=0_{E}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c499469deb60d7e7238f23c897491dc0_l3.png)
Mais cette dernière égalité s’écrit aussi :
![Rendered by QuickLaTeX.com \[\alpha\,y_{1}-\sum_{i=2}^{n+2}\,\mu_{i}\,y_{i}=0_{E}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b07d6cbb828a2fdc09166952e7e2c414_l3.png)
où l’on a posé
![Rendered by QuickLaTeX.com \[\alpha=\sum_{i=2}^{n+2}\,\mu_{i}\frac{\lambda_{i,n+1}}{\lambda_{1,n+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-58be5c443dd32c05cba36ccc826acf82_l3.png)
La famille

- Soient
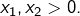 L’inégalité
L’inégalité 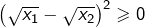 donne, après développement :
donne, après développement :![Rendered by QuickLaTeX.com \[\sqrt{x_{1}x_{2}}\leqslant\frac{x_{1}+x_{2}}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e2f9b13b88a3e76d7ff0b2be828b7f9c_l3.png)
- On notera
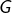 la moyenne géométrique de
la moyenne géométrique de 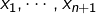 :
:![Rendered by QuickLaTeX.com \[G=\left(\prod_{i=1}^{n+1}x_{i}\right)^{1/\left(n+1\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-df02f4866d6cea6cd2f0ddd3c196d26d_l3.png)
a) Si ![]() pour tout
pour tout ![]() alors
alors ![]()
b) Par hypothèse, il existe ![]() tel que
tel que ![]()
Supposons par exemple ![]() Si l’on avait
Si l’on avait ![]() pour tout
pour tout ![]() il en résulterait (par sommation d’inégalités) :
il en résulterait (par sommation d’inégalités) :
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n+1}x_{k}<\left(n+1\right)A\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-df4b57c73c2f42d9cf6a25ef5e14e841_l3.png)
Il existe donc ![]() tel que
tel que ![]()
c) Avec ce qui précède, on voit que ![]() c’est-à-dire
c’est-à-dire
![]()
![]()
d) On peut toujours supposer ![]() quitte à échanger les termes
quitte à échanger les termes ![]() et
et ![]() dans la liste (ce n’est pas essentiel mais cela va simplifier la présentation). L’hypothèse de récurrence appliquée à la liste
dans la liste (ce n’est pas essentiel mais cela va simplifier la présentation). L’hypothèse de récurrence appliquée à la liste ![]() donne :
donne :
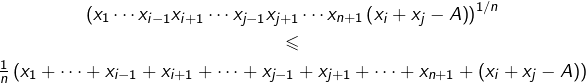
Dans cette dernière inégalité, le membre de droite (on devrait dire « le membre du haut », mais bon) vaut :
![]()
![]()
donc, d’après le point c) :
![]()
et finalement
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
