Solutions - Exercices sur racines carrées - 01

Solutions détaillées de neuf exercices sur la notion de racine carrée (fiche 01).
Cliquer ici pour accéder aux énoncés.

On commence par écrire :

$98=2\times7^{2}\qquad\text{et}\qquad125=5\times5^{2}$

d’où l’on déduit :

$A=\sqrt{\frac{2\times7^{2}}{5\times5^{2}}}=\frac{\sqrt{2\times7^{2}}}{\sqrt{5\times5^{2}}}=\frac{7\sqrt{2}}{5\sqrt{5}}$

Afin de mettre le résultat sous la forme d’une fraction à dénominateur entier (ce qui est recommandé), on multiplie numérateur et dénominateur par $\sqrt{5},$ ce qui donne finalement :

$\boxed{A=\frac{7\sqrt{10}}{25}}$

Ensuite, on voit que :

$B=\frac{\sqrt{5\times5^{2}\sqrt{16^{2}}}}{\sqrt{\frac{3}{5}}}=\sqrt{5\times5^{2}\times4^{2}}\times\sqrt{\frac{5}{3}}=\sqrt{5}\times20\times\frac{\sqrt{5}}{\sqrt{3}}=\frac{100}{\sqrt{3}}$

c’est-à-dire :

$\boxed{B=\frac{100\sqrt{3}}{3}}$

On cherche les $k\in\mathbb{N}$ vérifiant :

$171\leqslant k^{2}\leqslant320\qquad\left(\star\right)$

c’est-à-dire (la fonction racine carrée étant croissante) :

$\sqrt{171}\leqslant k\leqslant\sqrt{320}$

Or, le plus petit carré parfait supérieur à $171$ est $196=14^{2}$ et le plus grand carré parfait inférieur à $320$ est $289=17^{2}.$

Par conséquent, la condition $\left(\star\right)$ équivaut à :

$14\leqslant k\leqslant17$

Le nombre cherché est donc $N=17-14+1,$ soit $\boxed{N=4}$

Remarque

Les carrés parfaits compris entre $171$ et $320$ sont $196,$ $225,$ $256$ et $289.$

On peut généraliser facilement. Considérons deux entiers naturels $A,B$ tels que $A<B.$ Pour tout entier positif $k,$ les conditions suivantes sont équivalentes :

$\begin{align*} A \leqslant k^{2} \leqslant B\\ \sqrt{A} \leqslant k \leqslant \sqrt{B}\\ \left\lceil \sqrt{A}\right\rceil \leqslant k \leqslant \left\lfloor \sqrt{B}\right\rfloor \end{align*}$

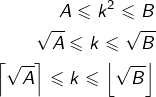
Précisons la notation utilisée. Etant donné un réel $X$ :

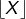$\left\lfloor X\right\rfloor$ désigne la partie entière par défaut de 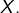$X.$ C’est le plus grand entier 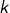$k$ tel que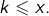 $k\leqslant x.$
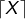$\left\lceil X\right\rceil$ désigne la partie entière par excès de 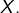$X.$ C’est le plus petit entier 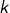$k$ tel que $k\geqslant x.$

Au final, le nombre de carrés parfaits compris entre $A$ et $B$ est $N=\left\lfloor \sqrt{B}\right\rfloor -\left\lceil \sqrt{A}\right\rceil +1.$

On observe que :

$C=\sqrt{2\times2^{2}\times2^{3}\times2^{4}\times2^{5}\times2^{6}\times2^{7}\times2^{8}}$

c’est-à-dire :

$C=\sqrt{2^{1+2+3+4+5+6+7+8}}$

On peut (mais ce n’est pas vraiment indispensable) exploiter le fait que, pour tout entier $n\geqslant1$ :

$1+2+\cdots+n=\frac{n\left(n+1\right)}{2}$

En particulier :

$1+2+3+4+5+6+7+8=\frac{8\times9}{2}=36$

et donc :

$C=\sqrt{2^{36}}=\sqrt{\left(2^{18}\right)^{2}}=2^{18}$

soit finalement :

$\boxed{C=262144}$

On va exploiter l’encadrement :

$\displaystyle{0\leqslant1+\frac{x}{2}-\sqrt{1+x}\leqslant\frac{x^{2}}{8}\qquad\left(\star\right)}$

qui est valable pour tout réel $x\geqslant0.$ Une autre façon de dire la même chose :

Si $x\geqslant0,$ alors $1+\frac{x}{2}$ est une valeur approchée de $\sqrt{1+x}$ à $\frac{x^{2}}{8}$ près.

En quoi cela nous aidera-t-il à trouver une valeur approchée de $\sqrt{25,05}$ ?

Tout simplement en observant que :
$25,05=25\times1,002$ et choisissant $x=0,002$ dans $\left(\star\right),$ ce qui donne :

$0\leqslant1,001-\sqrt{1,002}\leqslant5\times10^{-7}$

et donc (en multipliant par 5) :

$0\leqslant5,005-\sqrt{25,05}\leqslant25\times10^{-7}=0,25\times10^{-5}$

Conclusion

$5,005$ est une valeur approchée de $\sqrt{25,05}$ à $0,25\times10^{-5}$ près par excès.

A la calculette, on trouve :

$\sqrt{25,05}\simeq 5,0049975025$

ce qui confirme notre estimation.

On va reconnaître, pour $A$ comme pour $B,$ une expression développée de la forme $a^{2}-2ab+b^{2}$ sous le symbole $\sqrt{\left.\qquad\right.}.$ L’astuce consiste à écrire :

$41-12\sqrt{5}=36-2\times6\sqrt{5}+\left(\sqrt{5}\right)^{2}=\left(6-\sqrt{5}\right)^{2}$

On en déduit aussitôt que $A=\left|6-\sqrt{5}\right|,$ c’est-à-dire (vu que $6>\sqrt{5}$ ) :

$\boxed{A=6-\sqrt{5}}$

De la même manière :

$37-20\sqrt{3}=25-20\sqrt{3}+12=\left(5-2\sqrt{3}\right)^{2}$

et donc, comme $5>2\sqrt{3}$ :

$\boxed{B=5-2\sqrt{3}}$

Méthode 1

Posons, pour tout $x\geqslant0$ :

$D\left(x\right)=1+\frac{x}{2}-\sqrt{1+x}$

On transforme cette expression avec la technique de l’expression conjuguée :

$D\left(x\right)=\frac{\left(1+\frac{x}{2}-\sqrt{1+x}\right)\left(1+\frac{x}{2}+\sqrt{1+x}\right)}{1+\frac{x}{2}+\sqrt{1+x}}$

c’est-à-dire :

$D\left(x\right)=\frac{\left(1+\frac{x}{2}\right)^{2}-1-x}{1+\frac{x}{2}+\sqrt{1+x}}=\frac{x^{2}}{4\left(1+\frac{x}{2}+\sqrt{1+x}\right)}$

Sous cette forme, il est évident que $D\left(x\right)\geqslant0.$ Maintenant, on minore le dénominateur en observant que:

$1+\frac{x}{2}\geqslant1\qquad\text{et}\qquad\sqrt{1+x}\geqslant1\qquad\text{d'où}\qquad1+\frac{x}{2}+\sqrt{1+x}\geqslant2$

et donc :

$D\left(x\right)\leqslant\frac{x^{2}}{8}$

Méthode 2

On étudie les variations de

$f:\left[0,+\infty\right[\rightarrow\mathbb{R},\thinspace x\mapsto\sqrt{1+x}-1-\frac{x}{2}+\frac{x^{2}}{8}$

Cette fonction est dérivable et, pour tout $x\geqslant0$ :

$f'\left(x\right)=\frac{1}{2\sqrt{1+x}}-\frac{1}{2}+\frac{x}{4}$

Dérivons encore un coup :

$f''\left(x\right)=-\frac{1}{4\left(1+x\right)^{3/2}}+\frac{1}{4}$

Après réduction au même dénominateur, on voit que cette dernière expression est du signe de $\left(1+x\right)^{3/2}-1,$ donc positive.

Ainsi $f'$ est croissante. Comme $f'\left(0\right)=0,$ on en déduit que $f'$ est à valeurs positives. Du coup, $f$ est croissante et, comme $f\left(0\right)=0,$ on voit que $f$ est aussi à valeurs positives : c’était la conclusion attendue.

Rappelons que la fonction racine carrée est croissante et que, par conséquent, si $x,y\geqslant0$ sont tels que $x^{2}\leqslant y^{2},$ alors $x\leqslant y.$

Comparons donc les carrés de $A$ et $B.$ On calcule d’abord :

$A^{2}=\left(\sqrt{13}+\sqrt{29}\right)^{2}=13+29+2\sqrt{13\times29}=42+2\sqrt{377}$

$B^{2}=\left(\sqrt{17}+\sqrt{24}\right)^{2}=17+24+2\sqrt{17\times24}=41+2\sqrt{408}$

puis on cherche le signe de :

$B^{2}-A^{2}=2\left(\sqrt{408}-\sqrt{377}\right)-1=\alpha-\beta$

où l’on a posé :

$\alpha=2\sqrt{408}\qquad\text{et}\qquad\beta=2\sqrt{377}+1$

Comparons les carrés (bis) !… On calcule donc :

$\alpha^{2}=4\times408=1632$

$\beta^{2}=4\times377+4\sqrt{377}+1=1509+4\sqrt{377}$

puis on cherche le signe de $\alpha^{2}-\beta^{2}=123-4\sqrt{377}$ .
Cette dernière quantité est du signe de : $123^{2}-16\times377=15129-6032>0$ .
On en déduit successivement que $\alpha^{2}-\beta^{2}>0,$ $\alpha-\beta>0,$ $B^{2}-A^{2}>0$ et enfin $B-A>0.$ Conclusion :

$\boxed{\sqrt{13}+\sqrt{29}<\sqrt{17}+\sqrt{24}}$

Pour tout $x\in\mathbb{R}$ : $\sqrt{x^{2}+1}>\sqrt{x^{2}},$ car la fonction racine carrée est strictement croissante. Autrement dit :

$\sqrt{x^{2}+1}>\left|x\right|$

De plus, par définition de la valeur absolue de $x$ (qui est, rappelons-le, le plus grand des deux nombres $x$ et $-x$ ) :

$\left|x\right|\geqslant-x$

Par conséquent :

$\sqrt{x^{2}+1}>-x$

c’est-à-dire :

$\boxed{\sqrt{x^{2}+1}+x>0}$

Comme $\sqrt{2}$ est irrationnel, l’application $\mathbb{Z}^{2}\rightarrow\mathbb{R},\left(a,b\right)\mapsto a+b\sqrt{2}$ est injective. Autrement dit, étant donné un réel de la forme $a+b\sqrt{2}$ avec $\left(a,b\right)\in\mathbb{Z}^{2},$ le couple $\left(a,b\right)$ est uniquement déterminé. Notons $\mathbb{Z}\left[\sqrt{2}\right]=\left\{ a+b\sqrt{2},\,\left(a,b\right)\in\mathbb{Z}^{2}\right\}$ et considérons l’application

$f:\mathbb{Z}\left[\sqrt{2}\right]\rightarrow\mathbb{Z}\left[\sqrt{2}\right],a+b\sqrt{2}\mapsto a-b\sqrt{2}$

On vérifie (calcul élémentaire, non détaillé) que :

$\forall\left(u,v\right)\in\mathbb{Z}\left[\sqrt{2}\right]^{2},\,f\left(uv\right)=f\left(u\right)\,f\left(v\right)\qquad\left(\diamondsuit\right)$

Etant donné $n\in\mathbb{N}^{\star}$ , la formule du binôme montre qu’il existe des entiers $a_{n},b_{n}\geqslant0$ tels que :

$\left(1+\sqrt{2}\right)^{n}=a_{n}+b_{n}\sqrt{2}\qquad\left(1\right)$

D’après $\left(\diamondsuit\right),$ il vient :

$\left(1-\sqrt{2}\right)^{n}=a_{n}-b_{n}\sqrt{2}\qquad\left(2\right)$

et donc, en multipliant $(1)$ et $(2)$ membre-à-membre :

$\left(-1\right)^{n}=a_{n}^{2}-2b_{n}^{2}$

Ainsi :

$\left(\sqrt{2}-1\right)^{n}=\left(-1\right)^{n}\left(1-\sqrt{2}\right)^{n}=\left(-1\right)^{n}\left(a_{n}-b_{n}\sqrt{2}\right)$

c’est-à-dire :

$\boxed{\left(\sqrt{2}-1\right)^{n}=\left(-1\right)^{n}\left(\sqrt{a_{n}^{2}}-\sqrt{a_{n}^{2}-\left(-1\right)^{n}}\right)}$

Si $n$ est pair, cette dernière expression s’écrit :
$\sqrt{a_{n}^{2}}-\sqrt{a_{n}^{2}-1}$
qui est de la forme voulue.
Sinon, elle s’écrit :
$\sqrt{a_{n}^{2}+1}-\sqrt{a_{n}^{2}}$
qui est aussi de la forme voulue.

Le résultat demandé est donc établi.

Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.

Partager cet article

Remarque

Conclusion

Méthode 1

Méthode 2

Laisser un commentaire Annuler la réponse