Solutions détaillées de neuf exercices sur la notion de produit scalaire (fiche 01).
Cliquer ici pour accéder aux énoncés.
Divers éléments théoriques sont disponibles dans cet article.

Traitons directement le cas général.
Soient ![]() et
et ![]() des réels tous distincts.
des réels tous distincts.
Pour tout ![]() , l’application :
, l’application :
![]()
Par conséquent, l’application :
![Rendered by QuickLaTeX.com \[\mathbb{R}_{n}\left[X\right]^{2}\rightarrow\mathbb{R},\thinspace\left(P\mid Q\right)\mapsto\sum_{i=0}^{n}P\left(a_{i}\right)Q\left(a_{i}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-54392c89f353e2af01bec27f464b361c_l3.png)
En outre, si ![]() c’est-à-dire si
c’est-à-dire si 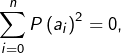 alors (somme nulle de réels positifs)
alors (somme nulle de réels positifs) ![]() pour tout
pour tout ![]()
Enfin, on sait que le seul élément de ![]() possédant
possédant ![]() racines est le polynôme nul.
racines est le polynôme nul.
Bref, on a bien affaire à un produit scalaire. Ensuite, la bonne idée est de penser à l’interpolation de Lagrange. Notons ![]() l’unique élément de
l’unique élément de ![]() vérifiant :
vérifiant :
![Rendered by QuickLaTeX.com \[L_{j}\left(a_{i}\right)=\left\{\begin{array}{cc}1 & \text{si }i=j\\\\0 & \text{sinon}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1e69f2f3a3242f6f771d953a52f8a0f6_l3.png)
![Rendered by QuickLaTeX.com \[ L_{j}=\prod_{{0\leqslant i\leqslant n\atop i\neq j}}\frac{X-a_{i}}{a_{j}-a_{i}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e6b3703d5576f92fa572620afc12c4e9_l3.png)
Il est classique que ![]() est une base de
est une base de ![]() En outre, pour tout
En outre, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\left(L{j}\mid L_{k}\right)=\sum_{i=0}^{n}\delta_{i,j}\delta_{i,k}=\delta_{j,k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cdcdaf78ddf4aa9e3c4d71a06244aee0_l3.png)
On montre d’abord la linéarité de ![]() Pour cela, on considère deux vecteurs
Pour cela, on considère deux vecteurs ![]() un réel
un réel ![]() et l’on espère prouver que :
et l’on espère prouver que :
![]()
Il faut bien voir que les deux membres de cette égalité sont des formes linéaires et, en particulier, des applications. On va donc se donner ![]() quelconque et prouver que :
quelconque et prouver que :
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left[\varphi\left(\lambda a+b\right)\right]\left(x\right) & \underset{\left(1\right)}{=} & \left(\lambda a+b\mid x\right)\\& \underset{\left(2\right)}{=} & \lambda\left(a\mid x\right)+\left(b\mid x\right)\\& \underset{\left(3\right)}{=} & \lambda\thinspace\left[\varphi\left(a\right)\right]\left(x\right)+\left[\varphi\left(b\right)\right]\left(x\right)\\& \underset{\left(4\right)}{=} & \left[\lambda\thinspace\varphi\left(a\right)+\varphi\left(b\right)\right]\left(x\right)\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-c960cc66d9ab01092393d5d0d682688d_l3.png)
Les égalités ![]() et
et ![]() découlent de la définition de
découlent de la définition de ![]() L’égalité
L’égalité ![]() provient de la linéarité à gauche du produit scalaire. Quant à l’égalité
provient de la linéarité à gauche du produit scalaire. Quant à l’égalité ![]() elle résulte de la définition de
elle résulte de la définition de ![]() où
où ![]() sont deux formes linéaires sur
sont deux formes linéaires sur ![]()
La linéarité de ![]() est établie. Plus formellement, on a prouvé que :
est établie. Plus formellement, on a prouvé que :
![]()
Pour montrer l’injectivité de ![]() il suffit de vérifier que son noyau est réduit au vecteur nul de
il suffit de vérifier que son noyau est réduit au vecteur nul de ![]()
Si ![]() alors
alors ![]() est la forme linéaire nulle, ce qui signifie que :
est la forme linéaire nulle, ce qui signifie que :
![]()
En particulier : ![]() et donc
et donc ![]() L’injectivité de
L’injectivité de ![]() est établie.
est établie.
Si ![]() est de dimension finie, alors
est de dimension finie, alors ![]() On peut donc affirmer, grâce au théorème du rang, que
On peut donc affirmer, grâce au théorème du rang, que ![]() est un isomorphisme.
est un isomorphisme.
Remarque
Cet isomorphisme est qualifié de canonique, pour indiquer qu’il a été défini de manière intrinsèque, c’est-à-dire sans utiliser une quelconque base de ![]()
Lorsque ![]() est de dimension infinie, l’application
est de dimension infinie, l’application ![]() n’est jamais surjective.
n’est jamais surjective.
En voici une démonstration, si vous êtes intéress(é)e.
Toutes les formes linéaires du type ![]() pour
pour ![]() sont continues. Ceci résulte de l’inégalité de Cauchy-Schwarz :
sont continues. Ceci résulte de l’inégalité de Cauchy-Schwarz :
![]()
Il suffit donc de prouver l’existence de formes linéaires discontinues pour conclure que ![]() n’est pas surjective.
n’est pas surjective.
Comme ![]() est de dimension infinie, il existe une suite
est de dimension infinie, il existe une suite ![]() de vecteurs de
de vecteurs de ![]() qui sont unitaires et linéairement indépendants.
qui sont unitaires et linéairement indépendants.
Notons ![]() et soit
et soit ![]() un supplémentaire de
un supplémentaire de ![]() dans
dans ![]() On définit une forme linéaire
On définit une forme linéaire ![]() sur
sur ![]() par les relations suivantes :
par les relations suivantes :
![]()
et
![]()
Cette forme linéaire est discontinue, puisqu’elle n’est pas bornée sur la sphère unité de ![]()
Voici maintenant un résultat moins précis, mais qui n’est déjà pas si mal…
L’espace ![]() des applications continues de
des applications continues de ![]() dans
dans ![]() est muni du produit scalaire défini par :
est muni du produit scalaire défini par :
![]()
On considère la forme linéaire » évaluation en ![]() » :
» :
![]()
Supposons qu’il existe ![]() tel que
tel que ![]() c’est-à-dire tel que :
c’est-à-dire tel que :
![]()
En choisissant ![]() on constate que :
on constate que :
![]()
L’application ![]() est continue, positive et d’intégrale nulle : c’est donc l’application nulle.
est continue, positive et d’intégrale nulle : c’est donc l’application nulle.
Il en résulte que ![]() est l’application nulle (nulle en tout point de
est l’application nulle (nulle en tout point de ![]() et donc aussi en
et donc aussi en ![]() par continuité). Mais ceci signifie que
par continuité). Mais ceci signifie que ![]() est la forme linéaire nulle, ce qui est absurde ! On a donc prouvé que
est la forme linéaire nulle, ce qui est absurde ! On a donc prouvé que ![]() ne possède aucun antécédent par
ne possède aucun antécédent par ![]() .
.
Preuve 1
Si ![]() l’inégalité à établir est vraie (c’est même une égalité) et la famille
l’inégalité à établir est vraie (c’est même une égalité) et la famille ![]() est liée.
est liée.
Supposons maintenant ![]() et posons, pour tout
et posons, pour tout ![]() :
:
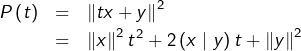
On voit que ![]() est un trinôme de signe constant, donc de discriminant négatif ou nul (rappelons qu’un trinôme de discriminant strictement positif possède deux racines distinctes, qu’il est du signe de son coefficient dominant à l’extérieur du segment limité par les racines et du signe contraire à l’intérieur).
est un trinôme de signe constant, donc de discriminant négatif ou nul (rappelons qu’un trinôme de discriminant strictement positif possède deux racines distinctes, qu’il est du signe de son coefficient dominant à l’extérieur du segment limité par les racines et du signe contraire à l’intérieur).
Ceci donne l’inégalité souhaitée.
Le cas d’égalité est celui où le discriminant est nul : il existe alors ![]() tel que
tel que ![]() c’est-à-dire
c’est-à-dire ![]() ou encore
ou encore ![]() La famille
La famille ![]() est donc liée.
est donc liée.
Preuve 2
Supposons ![]() et
et ![]() non nuls. On observe que :
non nuls. On observe que :
![Rendered by QuickLaTeX.com \[ 0\leqslant\frac{1}{2}\left\Vert \frac{x}{\left\Vert x\right\Vert }-\frac{\epsilon y}{\left\Vert y\right\Vert }\right\Vert ^{2}=\frac{1}{2}\left[\left\Vert \frac{x}{\left\Vert x\right\Vert }\right\Vert ^{2}+\left\Vert \frac{\epsilon y}{\left\Vert y\right\Vert }\right\Vert ^{2}-2\frac{\epsilon}{\left\Vert x\right\Vert \left\Vert y\right\Vert }\left(x\mid y\right)\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-774a993d12be63707237e87c3ca4388b_l3.png)
![]()
Or, ![]() par définition de
par définition de ![]() et donc :
et donc :
![]()
En cas d’égalité, on a :
![]()

Fixons une base orthonormale ![]() de
de ![]() Soit
Soit ![]() une forme bilinéaire.
une forme bilinéaire.
Pour tout ![]() en décomposant
en décomposant ![]() dans
dans ![]() sous la forme :
sous la forme :
![Rendered by QuickLaTeX.com \[ x=\sum_{i=1}^{n}x_{i}e_{i}\qquad\text{et}\qquad y=\sum_{j=1}^{n}y_{j}e_{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a574984671724fb987916fd8614f6dd2_l3.png)
![Rendered by QuickLaTeX.com \[\varphi\left(x,y\right)=\sum_{i=1}^{n}\sum_{j=1}^{n}x_{i}y_{j}\thinspace\varphi\left(e_{i},e_{j}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-133b7812939a12b4df805b2a1d6cecac_l3.png)
Notons ![]() D’après l’inégalité triangulaire :
D’après l’inégalité triangulaire :
![Rendered by QuickLaTeX.com \[\left|\varphi\left(x,y\right)\right|\leqslant\alpha\sum_{i=1}^{n}\sum_{j=1}^{n}\left|x_{i}\right|\left|y_{j}\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0bb1903a860d8709089d44330c0f78d3_l3.png)
![Rendered by QuickLaTeX.com \[\left|\varphi\left(x,y\right)\right|\leqslant\alpha\left(\sum_{i=1}^{n}\left|x_{i}\right|\right)\left(\sum_{j=1}^{n}\left|y_{j}\right|\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6c10113734a8cb4c50462c40fdc76d2d_l3.png)
Mais d’après l’inégalité de Cauchy-Schwarz :
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{n}\left|x_{i}\right|=\sum_{i=1}^{n}1\times\left|x_{i}\right|\leqslant\left(\sum_{i=1}^{n}1^{2}\right)^{1/2}\left(\sum_{i=1}^{n}x_{i}^{2}\right)^{1/2}=\sqrt{n}\left\Vert x\right\Vert \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-eefac58b6e8ef2b072059237b3a46c9b_l3.png)
![Rendered by QuickLaTeX.com \[ \sum_{j=1}^{n}\left|y_{j}\right|\leqslant\sqrt{n}\left\Vert y\right\Vert \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9f4b1bdf2f39aa961b45f8cada6f7d1f_l3.png)
Finalement, en posant ![]() :
:
![]()
Remarque
L’inégalité établie ci-dessus exprime la continuité de la forme bilinéaire ![]() .
.
D’une manière générale, étant donné un ![]() -espace vectoriel normé et une forme
-espace vectoriel normé et une forme ![]() -linéaire
-linéaire ![]() sur
sur ![]() (c’est-à-dire : une application de
(c’est-à-dire : une application de ![]() dans
dans ![]() qui est « linéaire par rapport à chaque variable »), on a l’équivalence entre les deux affirmations suivantes :
qui est « linéaire par rapport à chaque variable »), on a l’équivalence entre les deux affirmations suivantes :
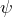 est continue
est continue- il existe un réel
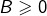 tel que :
tel que :
pour tout![Rendered by QuickLaTeX.com \[\vert\psi\left(x_1,\cdots,x_p\right)\vert\leqslant B\Vert x_1\Vert\cdots\Vert x_p\Vert\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-417adfc55e37cae04d4cd107838ac497_l3.png)
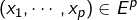 .
.
On peut montrer que si ![]() est de dimension finie, la continuité d’une forme multilinéaire est automatique et ce, quelle que soit la norme choisie (rappelons qu’en dimension finie, les normes sur un
est de dimension finie, la continuité d’une forme multilinéaire est automatique et ce, quelle que soit la norme choisie (rappelons qu’en dimension finie, les normes sur un ![]() -espace vectoriel sont toutes équivalentes).
-espace vectoriel sont toutes équivalentes).
L’exercice n’aborde qu’un cas très particulier de cette situation (dimension 2 et norme issue d’un produit scalaire), mais de façon directe.

Soient ![]() des vecteurs unitaires de
des vecteurs unitaires de ![]() D’après l’inégalité de Cauchy-Schwarz :
D’après l’inégalité de Cauchy-Schwarz :
![]()
D’autre part :
![Rendered by QuickLaTeX.com \begin{eqnarray*}0 & \leqslant & \left\Vert x+y+z\right\Vert ^{2}\\& = & \left\Vert x\right\Vert ^{2}+\left\Vert y\right\Vert ^{2}+\left\Vert z\right\Vert ^{2}+2\left[\left(x\mid y\right)+\left(y\mid z\right)+\left(z\mid x\right)\right]\\& = & 3+2\thinspace f\left(x,y,z\right)\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-d70ea3ea084aac54723139d3241187b4_l3.png)
et donc :
![]()
Dans ![]() l’inégalité de gauche est réalisée si l’on choisit :
l’inégalité de gauche est réalisée si l’on choisit :
![]()
Et l’inégalité de droite est réalisée dès que ![]()
Remarque
![]() est une partie compacte de
est une partie compacte de ![]() et
et ![]() est continue. On pouvait donc affirmer, a priori, que
est continue. On pouvait donc affirmer, a priori, que ![]() est bornée et atteint ses bornes.
est bornée et atteint ses bornes.
Soit ![]() continue, positive et d’intégrale nulle.
continue, positive et d’intégrale nulle.
Supposons ![]() non nulle, c’est-à-dire :
non nulle, c’est-à-dire : ![]()
On peut d’ailleurs, en raison de la continuité de ![]() en
en ![]() et en
et en ![]() considérer que
considérer que ![]()
Par continuité de ![]() en
en ![]() il existe
il existe ![]() tel que
tel que ![]() et, pour tout
et, pour tout ![]() :
:
![]()
![]()
![]()
Il en résulte que :
![]()
Lemme
Si ![]() est continue, positive et d’intégrale nulle, alors
est continue, positive et d’intégrale nulle, alors ![]()
Dans cet énoncé, on peut bien sûr remplacer l’intervalle ![]() par un segment quelconque.
par un segment quelconque.
Considérons maintenant ![]() continue et strictement positive. Il est clair que
continue et strictement positive. Il est clair que
![]()
![]()
![]()
Voici maintenant la » bonne » version de ce résultat, avec des hypothèses minimales sur ![]() (qui est appelée fonction poids,… weight en anglais).
(qui est appelée fonction poids,… weight en anglais).
On note ![]() . C’est l’image réciproque par
. C’est l’image réciproque par ![]() du singleton
du singleton ![]() autrement dit l’ensemble des valeurs en lesquelles
autrement dit l’ensemble des valeurs en lesquelles ![]() s’annule.
s’annule.
Proposition
![]()
Rappelons que l’intérieur de ![]() noté
noté ![]() est l’ensemble des réels
est l’ensemble des réels ![]() vérifiant :
vérifiant :
![]()
Dire que ![]() est d’intérieur vide signifie que
est d’intérieur vide signifie que ![]() ne contient aucun intervalle non trivial.
ne contient aucun intervalle non trivial.
Preuve de ![]()
Par contraposée. Supposons ![]() et soient
et soient ![]() tels que
tels que ![]()
Considérons une application ![]() nulle en dehors de
nulle en dehors de ![]() et ne s’annulant pas dans
et ne s’annulant pas dans ![]()
Par exemple :
![Rendered by QuickLaTeX.com \[ f:\left[a,b\right]\rightarrow\mathbb{R},\thinspace t\mapsto\left\{\begin{array}{cc} 0 & \text{si }t\leqslant\alpha\text{ ou }t\geqslant\beta\\\\\left(t-\alpha\right)\left(\beta-t\right) & \text{si }\alpha<t<\beta\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-571bdc33e1ea9cca529f1bd15bbafa3d_l3.png)
Alors ![]() bien que
bien que ![]() ce qui montre que
ce qui montre que ![]() n’est pas définie positive.
n’est pas définie positive.
Preuve de ![]()
Encore par contraposée. Par hypothèse, il existe ![]() vérifiant
vérifiant ![]()
Vue la continuité de ![]() il existe un segment
il existe un segment ![]() ainsi que
ainsi que ![]() tels que :
tels que :
![]()
On constate alors que :
![]()
Ainsi, ![]()
Passer en revue les trois axiomes de normes va poser une sérieuse difficulté technique pour l’inégalité triangulaire.
Montrons plutôt qu’il existe un produit scalaire sur ![]() pour lequel
pour lequel ![]() n’est autre que la norme euclidienne associée.
n’est autre que la norme euclidienne associée.
Posons, pour tout ![]() :
:
![]()
Il est facile de voir que ![]() est une forme bilinéaire, symétrique et positive.
est une forme bilinéaire, symétrique et positive.
En outre, si ![]() alors (somme nulle de réels positifs) :
alors (somme nulle de réels positifs) :
![Rendered by QuickLaTeX.com \[ \left\{\begin{array}{ccccc} f\left(0\right) & = & 0\\ f'\left(1\right) & = & 0\\ \int_{0}^{1}f''\left(t\right)^{2}\thinspace dt & = & 0 & & \left(\star\right) \end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a4f69a75869520cd5c1dcd16bf16911b_l3.png)
D’après le lemme démontré au début de l’exercice n° 6, la condition ![]() impose
impose ![]() c’est-à-dire qu’il existe
c’est-à-dire qu’il existe ![]() tel que :
tel que :
![]()
Mais ![]() et
et ![]() donc
donc ![]() et finalement
et finalement ![]() est l’application nulle. Ceci prouve le caractère défini positif.
est l’application nulle. Ceci prouve le caractère défini positif.
Remarque
On s’appuie ici sur un résultat de cours : si ![]() est un
est un ![]() espace vectoriel muni d’un produit scalaire, alors l’application
espace vectoriel muni d’un produit scalaire, alors l’application ![]() est une norme. Le seul point non trivial dans cette affirmation concerne l’inégalité triangulaire. Celle-ci découle de l’inégalité de Cauchy-Schwarz.
est une norme. Le seul point non trivial dans cette affirmation concerne l’inégalité triangulaire. Celle-ci découle de l’inégalité de Cauchy-Schwarz.

Suivons les indications proposées.
On définit une produit scalaire sur ![]() en posant :
en posant :
![]()
Détail de cette affirmation
Cette intégrale impropre est convergente car (d’après la propriété des croissances comparées) :
![]()
![]()
Par ailleurs, il s’agit bien d’un produit scalaire. Bilinéarité, symétrie, positivité sont évidentes et de plus, si ![]() alors :
alors :
![]()
Enfin, ![]() est un polynôme possédant une infinité de racines et c’est donc le polynôme nul.
est un polynôme possédant une infinité de racines et c’est donc le polynôme nul.
Par commodité, on calcule une fois pour toutes :
![]()
D’après la théorie générale présentée à la section 3 de cet article :
![]()
Pour calculer cela, commençons par expliciter une base orthogonale ![]() de
de ![]()
On peut partir de la base canonique ![]() et l’orthogonaliser.
et l’orthogonaliser.
On trouve après quelques petits calculs :
![]()
Détail des « petits calculs » 🙂
Cherchons ![]()
![]() et
et ![]() sous la forme :
sous la forme :
![]()
![]()
![]()
Alors :
![]()
Ensuite :
![]()
et
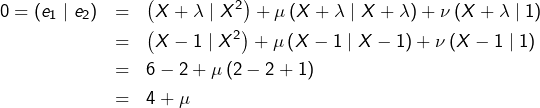
imposent
On s’appuie ensuite sur les deux formules :
![]()
et
![Rendered by QuickLaTeX.com \[ \left\Vert p_{F}\left(X^{3}\right)\right\Vert ^{2}=\frac{\left(X^{3}\mid e_{0}\right)^{2}}{\left\Vert e_{0}\right\Vert ^{2}}+\frac{\left(X^{3}\mid e_{1}\right)^{2}}{\left\Vert e_{1}\right\Vert ^{2}}+\frac{\left(X^{3}\mid e_{2}\right)^{2}}{\left\Vert e_{2}\right\Vert ^{2}}\qquad\left(\diamondsuit\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cff532379c999a0aa6961f2c96d3a40f_l3.png)
L’égalité ![]() résulte de la formule de Pythagore (les vecteurs
résulte de la formule de Pythagore (les vecteurs ![]() et
et ![]() sont orthogonaux).
sont orthogonaux).
L’égalité ![]() découle de l’expression en base orthonormale du projeté orthogonal sur
découle de l’expression en base orthonormale du projeté orthogonal sur ![]() d’un vecteur de
d’un vecteur de ![]() à savoir :
à savoir :
![Rendered by QuickLaTeX.com \[ p_{F}\left(X^{3}\right)=\frac{\left(X^{3}\mid e_{0}\right)}{\left\Vert e_{0}\right\Vert ^{2}}\thinspace e_{0}+\frac{\left(X^{3}\mid e_{1}\right)}{\left\Vert e_{1}\right\Vert ^{2}}\thinspace e_{1}+\frac{\left(X^{3}\mid e_{2}\right)}{\left\Vert e_{2}\right\Vert ^{2}}\thinspace e_{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-376f35088a9202c6265d2071e58eb240_l3.png)
Calculons quelques produits scalaires utiles :
![]()
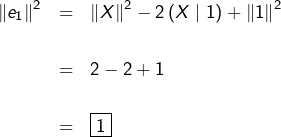
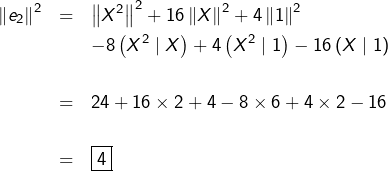
![]()
ainsi que :
![]()
![]()
![]()
On voit maintenant que :
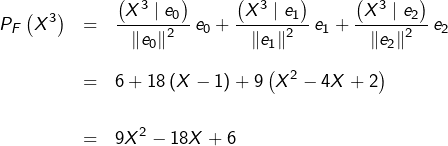
et :
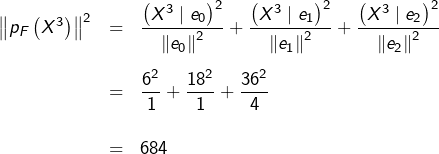
En conclusion :
![Rendered by QuickLaTeX.com \[ \boxed{\inf_{\left(a,b,c\right)\in\mathbb{R}^{3}}\int_{0}^{+\infty}\left(t^{3}-\left(at^{2}+bt+c\right)\right)e^{-t}\thinspace dt=36}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0147eb6a3a034ec10d32d5e5bc8b1a36_l3.png)
et cette borne inférieure est atteinte pour :
![]()

Soit ![]() Considérons l’application :
Considérons l’application :
![]()
![]()
L’application ![]() est continue car
est continue car ![]() lipschitzienne donc continue (pour une explication, voir ce passage d’une vidéo consacrée à une propriété de convexité de la distance à une partie d’un espace normé). Il s’ensuit que
lipschitzienne donc continue (pour une explication, voir ce passage d’une vidéo consacrée à une propriété de convexité de la distance à une partie d’un espace normé). Il s’ensuit que ![]() est aussi continue.
est aussi continue.
Comme ![]() alors
alors ![]() c’est-à-dire :
c’est-à-dire :
![]()
Le lemme habituel (cf. début de l’exercice n° 6 plus haut) s’applique et montre que ![]()
Ainsi, ![]() s’annule en tout point où
s’annule en tout point où ![]() ne s’annule pas. Or
ne s’annule pas. Or ![]() est fermé, et donc
est fermé, et donc ![]() Ainsi
Ainsi ![]()
Ceci montre que ![]() et l’inclusion réciproque est évidente.
et l’inclusion réciproque est évidente.
Remarque
Il n’est pas restrictif de supposer ![]() fermé puisque, pour toute partie
fermé puisque, pour toute partie ![]() de
de ![]() :
:
![]()
En effet ![]() donc
donc ![]()
Par ailleurs, si ![]() s’annule en tout point de
s’annule en tout point de ![]() alors
alors ![]() s’annule sur l’adhérence de
s’annule sur l’adhérence de ![]() par continuité.
par continuité.
Il en résulte que :
![]()
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
