Indications - Exercices sur le produit scalaire - 01

Indications pour démarrer les exercices sur la notion de produit scalaire (fiche 01).
Cliquer ici pour accéder aux énoncés.

Pour généraliser, considérer $a_{0},\cdots,a_{n}\in\mathbb{R}$ tous distincts et poser :

$\forall\left(P,Q\right)\in\mathbb{R}_{n}\left[X\right]^{2},\quad\left(P\mid Q\right)=\sum_{i=0}^{n}P\left(a_{i}\right)Q\left(a_{i}\right)$

Il faut commencer par prouver (sans faire d’hypothèse de dimension sur $E)$ que $\varphi$ est linéaire et montrer ensuite que $\varphi$ injective.

Attention de ne pas confondre $\varphi$ et $\varphi\left(a\right)$ …

⇨ Lorsque $E$ est supposé de dimension finie, on peut ensuite établir la surjectivité de $\varphi,$ mais de manière indirecte.

⇨ Pour le cas où $E$ est dimension infinie, l’exemple suivant pourra être étudié :

$E$ est l’espace des applications continues de $\left[0,1\right]$ dans $\mathbb{R},$ muni du produit scalaire défini par

$\forall\left(f,g\right)\in E^{2},\;\left(f\mid g\right)=\int_{0}^{1}f\left(t\right)\thinspace g\left(t\right)\thinspace dt$

Soit $L$ la forme linéaire sur $E$ définie par :

$\forall f\in E,\thinspace L\left(f\right)=f\left(0\right)$

On peut montrer montrer que $L$ ne possède aucun antécédent par $\varphi.$ A vous de jouer !

Pour la preuve 1

Si $x\neq0_{E},$ alors $P$ est un trinôme de signe constant. Que dire alors de son discriminant ?

Pour la preuve 2

Le développement de l’expression proposée doit donner

$1-\frac{\epsilon\left(x\mid y\right)}{\left\Vert x\right\Vert \left\Vert y\right\Vert }$

Sans oublier qu’on connaît le signe de cette expression !

Choisir une base orthonormale $\left(e_{1},\cdots,e_{n}\right)$ puis développer $\varphi\left(x,y\right)$ par bilinéarité, après avoir exprimé les vecteurs $x$ et $y$ dans cette base. Au cours de la majoration de $\left|\varphi\left(x,y\right)\right|,$ une expression du type $\sum_{1\leqslant i,j\leqslant n}x_{i}y_{j}$ doit apparaître : il faudra la factoriser.

Pour majorer, on peut penser à Cauchy-Schwarz.

Pour minorer, je vous suggère de développer $\Vert x+y+z\Vert^2$ .

La première partie de la question constitue un lemme classique de calcul intégral. Voici comment l’aborder …

On suppose $f:\left[0,1\right]\rightarrow\mathbb{R}$ continue, positive et d’intégrale nulle. Pour montrer que $f$ est identiquement nulle, on suppose le contraire, à savoir qu’il existe $c\in\left[0,1\right]$ tel que $f\left(c\right)>0.$ On peut même supposer que $c\in\left]0,1\right[$ (pourquoi ?).

On justifie alors l’existence d’un segment $\left[c-\alpha,c+\alpha\right],$ contenu dans $\left[0,1\right]$ et tel que $f\left(t\right)\geqslant\frac{1}{2}f\left(c\right)$ pour tout $t\in\left[c-\alpha,c+\alpha\right],$ ce qui va engendrer une contradiction.

Etant donnés un $\mathbb{R}-$ espace vectoriel $E$ et une application $N:E\rightarrow\mathbb{R}^{+},$ on dit que $N$ est une norme sur $E$ lorsque :

[ homogénéïté ]

$\forall\left(\lambda,x\right)\in\mathbb{R}\times E,\thinspace N\left(\lambda x\right)=\left|\lambda\right|\thinspace N\left(x\right)$

[ inégalité triangulaire ]

$\forall\left(x,y\right)\in E^{2},\thinspace N\left(x+y\right)\leqslant N\left(x\right)+N\left(y\right)$

[ condition de séparation ]

$\forall x\in E,\thinspace N\left(x\right)=0\Rightarrow x=0_{E}$

On doit pouvoir vérifier chacun de ces trois points (très facilement pour deux d’entre eux, et … moins facilement pour le troisième !).

Mais il y a peut-être un meilleur point de vue … Regardez donc l’intitulé de cette fiche d’exercices !

Si l’on considère :

$E=\mathbb{R}_{3}\left[X\right],$ l’espace des polynômes de degré inférieur ou égal à 3,
le produit scalaire défini sur 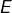$E$ par :
$\forall\left(P,Q\right)\in E^{2},\thinspace\left(P\mid Q\right)=\int_{0}^{+\infty}P\left(t\right)Q\left(t\right)e^{-t}\thinspace dt$
le sous-espace $F=\mathbb{R}_{2}\left[X\right],$
et le polynôme $P=X^{3}\in E$

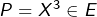
alors la quantité :

$\varphi\left(a,b,c\right)=\int_{0}^{+\infty}\left(t^{3}-at^{2}-bt-c\right)^{2}e^{-t}\thinspace dt$

s’interprète comme le carré de la distance de $P$ au polynôme $aX^{2}+bX+c,$
qui parcourt $F$ lorsque $\left(a,b,c\right)$ parcourt $\mathbb{R}^{3}.$

On cherche à minimiser cette distance …

Pour les pré-requis théoriques, on pourra se reporter à cet article et, tout particulièrement, à la section 3 de celui-ci.

Si $f\in\left(V_{A}\right)^{\bot},$ alors $f$ est en particulier orthogonale à …. ?

Penser à faire intervenir la fonction » distance à A « , qui est continue (pourquoi ?).

Partager cet article