

Les critères de divisibilité utilisés pour cet exercice sont présentés dans cet article.
On calcule successivement, avec la règle « ![]() » :
» :

donc :
![]()
puis avec la règle «

donc :
![]()
puis avec la règel «

donc :
![]()
et enfin, avec la règle «

donc :
![]()

![]() est évidemment un multiple de 4 vu que
est évidemment un multiple de 4 vu que ![]() C’est un multiple de 3 puisque la somme de ses chiffres l’est (cf. exercice 3 ci-dessous). C’est aussi un multiple de 11 puisque la somme alternée de ses chiffres l’est (elle vaut 0). Enfin, c’est un multiple de 7 et de 13 puisque
C’est un multiple de 3 puisque la somme de ses chiffres l’est (cf. exercice 3 ci-dessous). C’est aussi un multiple de 11 puisque la somme alternée de ses chiffres l’est (elle vaut 0). Enfin, c’est un multiple de 7 et de 13 puisque ![]() est multiple de 7 et de 13 (voir les règles
est multiple de 7 et de 13 (voir les règles ![]() et
et ![]() dans cet article).
dans cet article).
A titre indicatif, voici la décomposition en facteurs premiers (DFP) de ![]() :
:
![]()
![]() est impair (donc certainement pas multiple de
est impair (donc certainement pas multiple de ![]() La somme de ses chiffres vaut
La somme de ses chiffres vaut ![]() qui n’est pas multiple de 3, donc
qui n’est pas multiple de 3, donc ![]() ne l’est pas non plus. Comme
ne l’est pas non plus. Comme ![]() n’est ni multiple de 7, ni de
n’est ni multiple de 7, ni de ![]() il en va de même pour
il en va de même pour ![]() Cependant, la somme alternée des chiffres de
Cependant, la somme alternée des chiffres de ![]() est nulle, donc
est nulle, donc ![]() est multiple de
est multiple de ![]()
Voici la DFP de ![]() :
:
![]()
![]()
Enfin, ![]() est pair, mais n’est pas multiple de
est pair, mais n’est pas multiple de ![]() car
car ![]() ne l’est pas. C’est un multiple de
ne l’est pas. C’est un multiple de ![]() puisque :
puisque :
![]()
Mais ce n’est un multiple d’aucun des entier
![]()

Considérons un entier ![]() et son écriture décimale :
et son écriture décimale :
![Rendered by QuickLaTeX.com \[n=\sum_{i=0}^{r}c_{i}\thinspace10^{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bd2fe195dde3b4999a6a0b65e3d176f7_l3.png)
avec comme d’habitude :
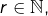
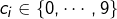 pour tout
pour tout 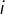
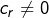
Comme ![]() alors
alors ![]() pour tout
pour tout ![]() et donc :
et donc :
![Rendered by QuickLaTeX.com \[\boxed{n\equiv\sum_{i=0}^{r}c_{i}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f4a02b863612c5c2384a88063960514c_l3.png)
Autrement dit :
tout entier naturel non nul est congru, modulo 3, à la somme de ses chiffres décimaux.
En particulier :
![]() est multiple de 3 si et seulement si la somme de ses chiffres l’est.
est multiple de 3 si et seulement si la somme de ses chiffres l’est.
Comme ![]() on peut, dans l’équivalence ci-dessus, remplacer 3 par 9.
on peut, dans l’équivalence ci-dessus, remplacer 3 par 9.

Si ![]() sont des entiers positifs, les multiples de
sont des entiers positifs, les multiples de ![]() se situant dans l’intervalle
se situant dans l’intervalle ![]() sont les entiers de la forme
sont les entiers de la forme ![]() avec
avec ![]() entier et tel que :
entier et tel que :
![]()
Vu le caractère entier de
![]()
Le nombre de tels entiers
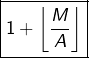
Il en résulte que si ![]() sont des entiers positifs tels que
sont des entiers positifs tels que ![]() alors les multiples de
alors les multiples de ![]() dans l’intervalle
dans l’intervalle ![]() sont au nombre de :
sont au nombre de :
![Rendered by QuickLaTeX.com \[\boxed{\left\lfloor \frac{M'}{A}\right\rfloor -\left\lfloor \frac{M-1}{A}\right\rfloor }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a63b32183354919aede0febc3d69241e_l3.png)
Il ne reste plus qu’à appliquer cette formule au cas particulier : ![]() Le nombre cherché est finalement :
Le nombre cherché est finalement :
![]()

Si ![]() alors :
alors :
![]()
![]()
Mais, dès que ![]() :
:
![]()

Quelques calculs conduisent à conjecturer que le chiffre des unités de ![]() est invariablement un
est invariablement un ![]() pour tout
pour tout ![]() En effet :
En effet :
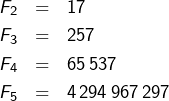
![]()
Supposons que, pour un certain ![]() on ait
on ait ![]() Alors :
Alors :
![]()

Dressons la table des cubes modulo ![]() :
:
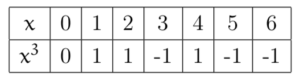
Si aucun des trois entiers ![]() n’est multiple de
n’est multiple de ![]() alors
alors ![]() donc
donc ![]()
Contraposée : si ![]() alors
alors ![]()
![]() ou
ou ![]() est multiple de
est multiple de ![]() et donc
et donc ![]() aussi.
aussi.

On peut factoriser
![Rendered by QuickLaTeX.com \[a^{n}-b^{n}=\left(a-b\right)\sum_{k=1}^{n}a^{k-1}b^{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2d49388f7ad14066f4f0bade02b24ab3_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}a^{k-1}b^{n-k}\equiv nb^{n-1}\equiv0\pmod{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0ebddb9067d13bc29d2e37727b7db981_l3.png)
![]()

On cherche les entiers ![]() vérifiant :
vérifiant :
![]()
![]()
- La condition
 est vérifiée lorsque
est vérifiée lorsque 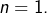
- Supposons que
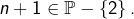 Alors :
Alors :![Rendered by QuickLaTeX.com \[n+1\nmid\left(n-1\right)!\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e73c3c7777442e3a444424b250ce5156_l3.png)
et![Rendered by QuickLaTeX.com \[n+1\nmid2\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-387f74ed6542a2964cf437549e38d3f3_l3.png)
donc, d’après le lemme d’Euclide, la condition n’est pas vérifiée.
n’est pas vérifiée. - Supposons maintenant que
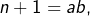 avec
avec 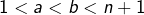 (ce qui impose
(ce qui impose  Alors
Alors 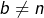 (puisque, dans le cas contraire :
(puisque, dans le cas contraire : 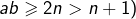 et donc
et donc  et
et 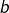 sont deux entiers distincts, inférieurs ou égaux à
sont deux entiers distincts, inférieurs ou égaux à  Il en résulte que
Il en résulte que 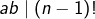 et
et  est vérifiée a fortiori.
est vérifiée a fortiori. - Si
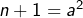 avec
avec  alors
alors 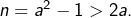 Ainsi,
Ainsi,  et
et 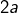 sont deux entiers distincts et inférieurs ou égaux à
sont deux entiers distincts et inférieurs ou égaux à  : leur produit
: leur produit 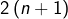 divise donc
divise donc  et donc a fortiori
et donc a fortiori  vérifie
vérifie  .
. - Enfin
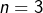 est solution.
est solution.
En conclusion, l’ensemble ![]() des solutions est constitué de 1 et des entiers supérieurs ou égaux à
des solutions est constitué de 1 et des entiers supérieurs ou égaux à ![]() dont le successeur n’est pas un nombre premier. En symboles :
dont le successeur n’est pas un nombre premier. En symboles :
![]()
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact
