Solutions détaillées de neuf exercices sur la dérivation des fonctions (fiche 02)
Cliquer ici pour accéder aux énoncés

L’application ![]() est définie et continue sur
est définie et continue sur ![]() dérivable au moins sur
dérivable au moins sur ![]()
Calculons son taux d’accroissement en 0. Pour tout ![]() :
:
![]()
![]()
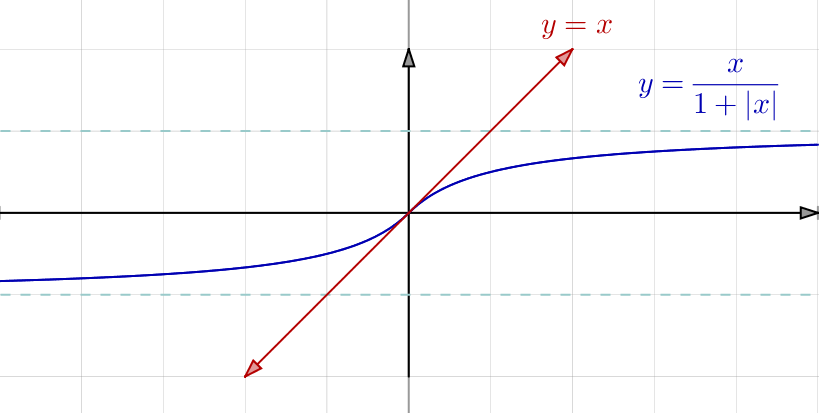
A titre indicatif, voici l’allure du graphe de ![]() qui est symétrique par rapport à l’origine (puisque
qui est symétrique par rapport à l’origine (puisque ![]() est impaire) et admet la première bissectrice pour tangente à l’origine. En outre, on peut signaler les deux asymptotes horizontales, d’équations
est impaire) et admet la première bissectrice pour tangente à l’origine. En outre, on peut signaler les deux asymptotes horizontales, d’équations ![]() et
et ![]()
Remarque
On sait que la composée de deux applications dérivables est dérivable.
L’intérêt de cet exercice est de montrer que la dérivabilité d’une composée ![]() n’implique pas celle de
n’implique pas celle de ![]() et de
et de ![]() Sauriez-vous trouver un exemple de couple
Sauriez-vous trouver un exemple de couple ![]() d’applications non dérivables tel que
d’applications non dérivables tel que ![]() soit dérivable ?
soit dérivable ?
Pour dévoiler une solution (parmi tant d’autres) … cliquer ici
Considérons la fonction indicatrice de ![]() :
:
![]()

L’application ![]() est dérivable et donc
est dérivable et donc ![]() aussi (composée d’applications dérivables). Pour tout
aussi (composée d’applications dérivables). Pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[f'\left(x\right)=\frac{\sqrt{1-x^{2}}-x\:{\displaystyle \frac{-2x}{2\sqrt{1-x^{2}}}}}{1-x^{2}}\:\arctan'\left(\frac{x}{\sqrt{1-x^{2}}}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-aaf3f342aed8b5643b6b895e3221ebac_l3.png)
![Rendered by QuickLaTeX.com \[f'\left(x\right)=\frac{1}{\left(1-x^{2}\right)^{3/2}}\:\frac{1}{1+{\displaystyle \frac{x^{2}}{1-x^{2}}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-72d252b1dfedfc2a3cf84cf059da03bc_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\forall x\in\left]-1,1\right[,\thinspace\arctan\left(\frac{x}{\sqrt{1-x^{2}}}\right)=\arcsin\left(x\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-688cce6af5cfa8bd79d67fbebc0af369_l3.png)
Remarque 1
Ce calcul intervient dans la preuve du lemme donnée à l’annexe 2 de cet article.
Remarque 2
Il existe une autre façon de traiter cet exercice, sans passer par un calcul de dérivée. Etant donné ![]() on considère l’unique
on considère l’unique ![]() tel que
tel que ![]() . On voit alors que :
. On voit alors que :
![]()

Supposons ![]() impaire et montrons que
impaire et montrons que ![]() est paire. Pour cela, posons pour tout
est paire. Pour cela, posons pour tout ![]() :
:
![]()
![]()
A présent, supposons ![]() paire. On pourrait penser que cette hypothèse va entraîner l’imparité de
paire. On pourrait penser que cette hypothèse va entraîner l’imparité de ![]() mais il n’en est rien (contre-exemple avec
mais il n’en est rien (contre-exemple avec ![]() Cependant, on peut adapter le calcul précédent et considérer l’application
Cependant, on peut adapter le calcul précédent et considérer l’application ![]() définie par :
définie par :
![]()
![]()
Remarque
Toutefois, si ![]() est paire et si de plus
est paire et si de plus ![]() alors
alors ![]() est impaire.
est impaire.

Supposons ![]() Pour tout
Pour tout ![]() et pour tout
et pour tout ![]() :
:
![]()
![]()
![]()
![]()

D’après la formule de Leibniz (voir cet article). Pour tout ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[f^{\left(n\right)}\left(x\right)=\sum_{k=0}^{n}\binom{n}{k}\exp^{\left(n-k\right)}\left(x\right)\sin^{\left(k\right)}\left(x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-20fa7077a20a64c024cce05ece12664e_l3.png)
![Rendered by QuickLaTeX.com \[f^{\left(n\right)}\left(x\right)=e^{x}\:\sum_{k=0}^{n}\binom{n}{k}\sin\left(x+\frac{k\pi}{2}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0c929038c22ecea4038d5bea4321e99f_l3.png)
![Rendered by QuickLaTeX.com \[f^{\left(n\right)}\left(0\right)=\sum_{k=0}^{n}\binom{n}{k}\sin\left(\frac{k\pi}{2}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-de6e295b04ab03b03d2fa70e6b4ac0f8_l3.png)
![Rendered by QuickLaTeX.com \[f^{\left(n\right)}\left(0\right)=\sum_{q=0}^{\left\lfloor \frac{n-1}{2}\right\rfloor }\binom{n}{2q+1}\sin\left(q\pi+\frac{\pi}{2}\right)=\sum_{q=0}^{\left\lfloor \frac{n-1}{2}\right\rfloor }\left(-1\right)^{q}\binom{n}{2q+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3bb7ed7c207104a3cf930eb0715b7185_l3.png)
Voici l’astuce, qui fait un petit crochet par le champ complexe … On observe que :
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{n}\binom{n}{k}i^{k}=\left(1+i\right)^{n}=2^{n/2}\thinspace e^{in\pi/4}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a675474effd1a280a84e3030b95dfa5f_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{q=0}^{\left\lfloor \frac{n-1}{2}\right\rfloor }\binom{n}{2q+1}\left(-1\right)^{q}=2^{n/2}\sin\left(\frac{n\pi}{4}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bd2f39fc059f139c98dd8660cfa201eb_l3.png)
![]()
Cela dit, puisqu’on s’est autorisé à passer par les complexes, autant y aller carrément ! On peut d’emblée observer que :
![]()
![]()
![]()

Lorsque ![]() est proche de 0, la variable d’intégration parcourt
est proche de 0, la variable d’intégration parcourt ![]() donc se promène aussi au voisinage de
donc se promène aussi au voisinage de ![]() et donc
et donc ![]() est voisin de 1. On peut donc conjecturer que
est voisin de 1. On peut donc conjecturer que ![]() se comporte, lorsque
se comporte, lorsque ![]() tend vers 0, comme :
tend vers 0, comme :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
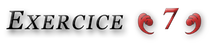
Pour ![]() l’intégrale
l’intégrale
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}\int_{0}^{T}\frac{\sin\left(t\right)}{x+t}\thinspace dt & = & \left[\frac{-\cos\left(t\right)}{x+t}\right]_{t=0}^{T}-\int_{0}^{T}\frac{\cos\left(t\right)}{\left(x+t\right)^{2}}\thinspace dt\\& = & \frac{1}{x}-\frac{\cos\left(T\right)}{x+T}-\int_{0}^{T}\frac{\cos\left(t\right)}{\left(x+t\right)^{2}}\thinspace dt \end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-5b915c61411127fc1e8c24b512320511_l3.png)
 est absolument convergente, elle est convergente et donc l’intégrale partielle
est absolument convergente, elle est convergente et donc l’intégrale partielle ![Rendered by QuickLaTeX.com \[ \lim_{T\rightarrow+\infty}\int_{0}^{T}\frac{\sin\left(t\right)}{x+t}\thinspace dt=\frac{1}{x}-\int_{0}^{+\infty}\frac{\cos\left(t\right)}{\left(x+t\right)^{2}}\thinspace dt \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-786d1bba51f96ecae8b7c00d76ad601f_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[ \boxed{\forall x>0,\thinspace f''\left(x\right)+f\left(x\right)=\frac{1}{x}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a1b668c3a1b52d4c60186df10a5c8efe_l3.png)

Comme ![]() est impair, alors
est impair, alors ![]() possède (au moins) une racine réelle
possède (au moins) une racine réelle ![]() L’hypothèse impose :
L’hypothèse impose :
![]()
![]()
(![]() )
) ![]()
![]()

On peut traiter cette question en combinant deux outils : d’une part, le lemme de Rolle et, d’autre part, le petit artifice technique suivant …
Si l’on pose, pour tout ![]() :
:
![]()
![]()
Supposons ![]() Par hypothèse, il existe des réels
Par hypothèse, il existe des réels ![]() tels que, pour tout
tels que, pour tout ![]()
![]() et donc
et donc ![]() En appliquant le lemme de Rolle à
En appliquant le lemme de Rolle à ![]() sur chacun des segments
sur chacun des segments ![]() on voit qu’il existe des réels
on voit qu’il existe des réels ![]() tels que :
tels que :
![]()
![]()
Lemme de Rolle étendu aux intervalles non bornés
Soit ![]() une application continue. On suppose que
une application continue. On suppose que ![]() est dérivable sur
est dérivable sur ![]() et que :
et que :
![]()
Si ![]() alors vu que
alors vu que ![]() est bornée, on voit que
est bornée, on voit que ![]() est bornée sur
est bornée sur ![]() et donc, en appliquant ce lemme à
et donc, en appliquant ce lemme à ![]() sur cet intervalle, on met en évidence un réel
sur cet intervalle, on met en évidence un réel ![]() tel que
tel que ![]() et
et ![]() d’où
d’où ![]()
De même, si ![]() on procède de même, mais sur l’intervalle
on procède de même, mais sur l’intervalle ![]() , ce qui donne l’existence d’un réel
, ce qui donne l’existence d’un réel ![]() tel que
tel que ![]() .
.
Bref, dans tous les cas, on constate que ![]() s’annule (au moins)
s’annule (au moins) ![]() fois.
fois.
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.

