Solutions détaillées de neuf exercices sur la dérivation des fonctions numériques (fiche 01).
Cliquer ici pour accéder aux énoncés.


Les calculs qui suivent sont valables pour tout ![]() sauf pour les fonctions
sauf pour les fonctions ![]() et
et ![]() (où il faut éviter qu’un dénominateur ne s’annule).
(où il faut éviter qu’un dénominateur ne s’annule).
➭ Pour ![]() aucun souci :
aucun souci :
![]()
➭ Deux méthodes pour ![]()
Méthode 1
On utilise la formule ![]() ce qui donne :
ce qui donne :
![]()
![]()
Méthode 2
On développe d’abord ![]() puis on dérive :
puis on dérive :
![]()
On termine en factorisant (il est souhaitable de factoriser l’expression obtenue pour une dérivée, vu qu’on s’intéresse généralement à son signe). Manifestement, la méthode 1 est plus efficace.
➭ A priori, on a encore deux méthodes à notre disposition pour ![]() .
.
La première consiste à utiliser la formule ![]() (pour
(pour ![]() ce qui donne :
ce qui donne :
![]()
La seconde consisterait à développer d’abord (par la formule du binôme) et à dériver ensuite, mais les calculs seraient pénibles et surtout, il serait acrobatique de factoriser l’expression obtenue ! Une situation analogue apparaît à l’exercice 2 pour le calcul de la dérivée de ![]()
Tenons-nous en donc à la méthode 1.
➭ Pour ![]() on utilise la formule
on utilise la formule ![]() :
:
![Rendered by QuickLaTeX.com \[ \boxed{D'\left(x\right)=-\frac{2}{\left(x+1\right)^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ab24d43fdd67eaf3c288093799da0bd5_l3.png)
Noter que l’on peut aussi écrire :
![]()
➭ Pour ![]() on utilise la formule
on utilise la formule ![]() pour obtenir :
pour obtenir :
![]()
![Rendered by QuickLaTeX.com \[ \boxed{E'\left(x\right)=\frac{1}{\left(x+2\right)^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a9686170dee07a46c8b073afa77e807e_l3.png)
On peut aussi observer que :
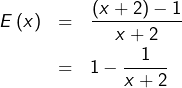
puis dériver à partir de là, ce qui évite d’avoir à se servir de la formule de dérivation d’un quotient.
➭ Enfin, pour ![]() il n’y a pas à hésiter : on applique la formule
il n’y a pas à hésiter : on applique la formule ![]() et on trouve :
et on trouve :
![]()
![Rendered by QuickLaTeX.com \[ \boxed{F'\left(x\right)=\frac{x^{2}\left(2x+3\right)}{\left(x+1\right)^{2}}}\qquad\left(\heartsuit\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c5a8c94626176f8cc7faa30581837ce9_l3.png)
On pourrait décomposer la fraction qui définit ![]() sous la forme :
sous la forme :
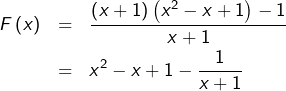
dériver :
![]()
réduire au même dénominateur :
![Rendered by QuickLaTeX.com \[ F'\left(x\right)=\frac{\left(2x-1\right)\left(x+1\right)^{2}+1}{\left(x+1\right)^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fddbccca7b89ab08ae2bb094a36a6688_l3.png)
factoriser le numérateur de la fraction obtenue :
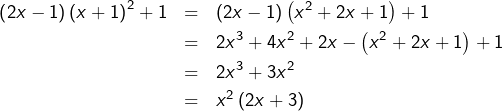
Au final, on retrouve bien ![]() C’est compliqué, mais pas inintéressant. Et surtout, il faut garder à l’esprit que la première étape de cette méthode (appelée décomposition en éléments simples) serait la bonne chose à faire si, au lieu d’avoir à trouver la dérivée de
C’est compliqué, mais pas inintéressant. Et surtout, il faut garder à l’esprit que la première étape de cette méthode (appelée décomposition en éléments simples) serait la bonne chose à faire si, au lieu d’avoir à trouver la dérivée de ![]() on devait plutôt en déterminer les primitives !
on devait plutôt en déterminer les primitives !

➭ Pour la fonction ![]() vous avez le choix entre deux options. Le plus simple, c’est de développer, ce qui donne :
vous avez le choix entre deux options. Le plus simple, c’est de développer, ce qui donne :
![]()
puis on dérive pour obtenir :
![]()
On peut aussi considérer que
![]()
d’où :
![]()
En appliquant la formule de dérivation d’un produit, on trouve donc :
![]()
conformément au premier calcul.
➭ Pour la fonction ![]() le plus simple consiste encore à développer :
le plus simple consiste encore à développer :
![]()
puis à dériver :
![]()
Une autre approche consisterait à voir
➭ Pour la fonction ![]() il serait maladroit de développer l’expression avant de dériver. En fait, pas seulement « maladroit », mais carrément infaisable ! Si vous ne me croyez pas, jugez plutôt …
il serait maladroit de développer l’expression avant de dériver. En fait, pas seulement « maladroit », mais carrément infaisable ! Si vous ne me croyez pas, jugez plutôt …
Voici la version développée :
![]()
Je vous rassure : je n’ai pas pas calculé ça à la main 🙂
Vous voyez ? Ce n’est pas raisonnable … En revanche, nous savons dériver une fonction du type ![]() Je vous remets la formule sous le nez …. si
Je vous remets la formule sous le nez …. si ![]() est dérivable et si
est dérivable et si ![]() alors :
alors :
![]()
En appliquant ceci, on voit que, pour tout
![]()
et voilà 🙂
➭ Pour la ![]() on applique la formule qui donne la dérivée de l’inverse, c’est-à-dire :
on applique la formule qui donne la dérivée de l’inverse, c’est-à-dire :
![]()
ce qui nous donne :
![Rendered by QuickLaTeX.com \[d'\left(x\right)=\boxed{-\frac{2x}{\left(x^{2}+1\right)^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5e9b4534f9187fddea64bb8ca6eea5d5_l3.png)
➭ Pour ![]() on dérive bien sûr le quotient
on dérive bien sûr le quotient ![]() avec :
avec :
![]()
d’où :
![]()
ce qui donne :
![Rendered by QuickLaTeX.com \[e'\left(x\right)=\frac{1\times\left(x^{4}+1\right)-x\times\left(4x^{3}\right)}{\left(1+x^{4}\right)^{2}}=\boxed{\frac{1-3x^{4}}{\left(1+x^{4}\right)^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a537bee48c221a29b6c646985e9e30ae_l3.png)
➭ Enfin, pour la ![]() on va commencer par développer numérateur et dénominateur, ce qui va s’accompagner pour chacun d’eux d’une petite simplification :
on va commencer par développer numérateur et dénominateur, ce qui va s’accompagner pour chacun d’eux d’une petite simplification :
![Rendered by QuickLaTeX.com \[f\left(x\right)={\displaystyle \frac{\left(x+1\right)^{3}-3x^{2}}{\left(2x+1\right)^{2}-4x^{2}}}=\frac{x^{3}+3x+1}{4x+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2b68497d86e458488a6e0471e8bee0a8_l3.png)
Ensuite, on pose :
![]()
d’où :
![]()
et donc :
![Rendered by QuickLaTeX.com \[f'\left(x\right)=\frac{\left(3x^{2}+3\right)\left(4x+1\right)-4\left(x^{3}+3x+1\right)}{\left(4x+1\right)^{2}}=\boxed{\frac{8x^{3}+3x^{2}-1}{\left(4x+1\right)^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0509795208b88aef865680937c4063db_l3.png)

On calcule, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ F'\left(x\right)=\frac{-\left(x^{2}+1\right)-\left(1-x\right)\left(2x\right)}{\left(x^{2}+1\right)^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-705d161e58e0be3d1c2f5a0f3c4d7c5f_l3.png)
![]()
Les racines du trinôme ![]() sont :
sont :
![]()
![]()
Ainsi, ![]() est :
est :
- croissante sur
![Rendered by QuickLaTeX.com \left]-\infty,\alpha\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cc8136f0aa3afaf07a6b46e5e51baa09_l3.png)
- décroissante sur
![Rendered by QuickLaTeX.com \left[\alpha,\beta\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5ad5ad60fe4c9987c56b811180858bf1_l3.png)
- croissante de nouveau sur
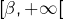
… Il ne manque plus grand chose pour compléter l’étude de ![]() .
.
Ses limites en ![]() et en
et en ![]() sont nulles.
sont nulles.
On peut calculer le signe de ![]() afin de déterminer les intervalles sur lesquels
afin de déterminer les intervalles sur lesquels ![]() est convexe ou concave. On obtient :
est convexe ou concave. On obtient :
![]()
- convexe sur
![Rendered by QuickLaTeX.com \left]-\infty,-1\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-922ad65f105fa1578a5f2b316af4e5bf_l3.png)
- concave sur
![Rendered by QuickLaTeX.com \left[-1,2-\sqrt{3}\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-34f45c58c8e0d1d6ad0c10f8ad23a234_l3.png)
- convexe sur
![Rendered by QuickLaTeX.com \left[2-\sqrt{3},2+\sqrt{3}\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-519ce8a0efe5ec124b9c27aebf35cc52_l3.png)
- concave sur
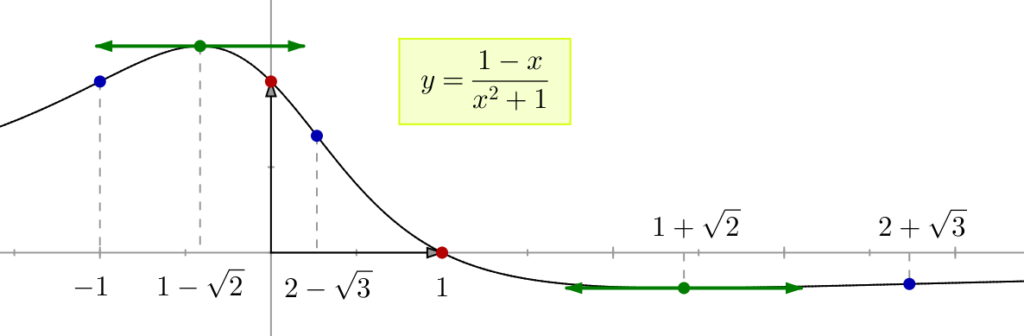
On peut aussi calculer les coordonnées des « points remarquables » du graphe de ![]() :
:
- points d’intersection avec les axes de coordonnées,
- points à tangente horizontale,
- points d’inflexion
Ces points sont respectivement représentés en rouge, vert et bleu sur l’illustration ci-dessous.

On pense à :
![]()
Par conséquent, les primitives de :
![]()
![]()
Il s’agit d’une petite récurrence très simple.
Pour ![]() c’est ni plus ni moins la formule de dérivation d’une somme de deux fonctions dérivables.
c’est ni plus ni moins la formule de dérivation d’une somme de deux fonctions dérivables.
Supposons maintenant la formule vraie au rang ![]() pour un certain
pour un certain ![]()
Soient alors ![]() des applications dérivables de
des applications dérivables de ![]() dans
dans ![]() Alors :
Alors :
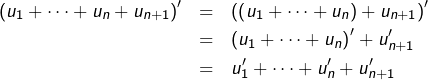
Là encore, on a affaire à une petite preuve par récurrence.
Pour ![]() il n’y a rien démontrer (la dérivée de
il n’y a rien démontrer (la dérivée de ![]() est égale … à la dérivée de
est égale … à la dérivée de ![]() ).
).
Supposons la formule vraie au rang ![]() pour un certain
pour un certain ![]() Alors :
Alors :
L’égalité ![]() résulte de la formule de dérivation d’un produit (à savoir
résulte de la formule de dérivation d’un produit (à savoir ![]() dans laquelle on a remplacé
dans laquelle on a remplacé ![]() par
par ![]() et
et ![]() par
par ![]()
L’égalité ![]() résulte de l’hypothèse de récurrence.
résulte de l’hypothèse de récurrence.
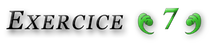
On voit que, pour tout ![]() :
:
![]()
![]()
On en déduit que :
![]()
![]()
![]()
Pour ![]() c’est connu :
c’est connu :
![]()
Pour ![]() voyons un peu …
voyons un peu …
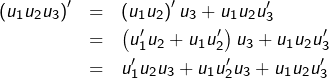
On conjecture alors la :
Proposition
Soit ![]() un intervalle. Pour tout entier
un intervalle. Pour tout entier ![]() et pour tout
et pour tout ![]() uplet
uplet ![]() de fonctions dérivables de
de fonctions dérivables de ![]() dans
dans ![]() la dérivée du produit
la dérivée du produit ![]() est la somme de
est la somme de ![]() termes, chaque terme étant le produit des
termes, chaque terme étant le produit des ![]() dans lequel un facteur a été dérivé et pas les autres.
dans lequel un facteur a été dérivé et pas les autres.
En clair :
![Rendered by QuickLaTeX.com \[ \left(\prod_{i=1}^{n}u_{i}\right)'=\sum_{k=1}^{n}u_{k}'\prod_{{1\leqslant i\leqslant n\atop i\neq k}}u_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-42b641e6252c82430f02c9387e906a37_l3.png)
Cette formule est vraie pour ![]() Supposons-la vraie au rang
Supposons-la vraie au rang ![]() pour un certain
pour un certain ![]()
Soient alors ![]() des fonctions dérivables sur
des fonctions dérivables sur ![]() On observe que :
On observe que :
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left(\prod_{i=1}^{n+1}u_{i}\right)' & = & \left[\left(\prod_{i=1}^{n}u_{i}\right)u_{n+1}\right]'\\& = & \left(\prod_{i=1}^{n}u_{i}\right)'u_{n+1}+\left(\prod_{i=1}^{n}u_{i}\right)u_{n+1}'\\& = & \left[\sum_{k=1}^{n}u_{k}'\prod_{{1\leqslant i\leqslant n\atop i\neq k}}u_{i}\right]u_{n+1}+\left(\prod_{i=1}^{n}u_{i}\right)u_{n+1}'\\& = & \sum_{k=1}^{n}u_{k}'\prod_{{1\leqslant i\leqslant n+1\atop i\neq k}}u_{i}+\left(\prod_{i=1}^{n}u_{i}\right)u_{n+1}'\\& = & \sum_{k=1}^{n+1}u_{k}'\prod_{{1\leqslant i\leqslant n+1\atop i\neq k}}u_{i}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-67db421e70a630cddec395d1db620cf9_l3.png)

L’abscisse d’un éventuel point d’intersection entre ces deux courbes est solution de l’équation : ![]()
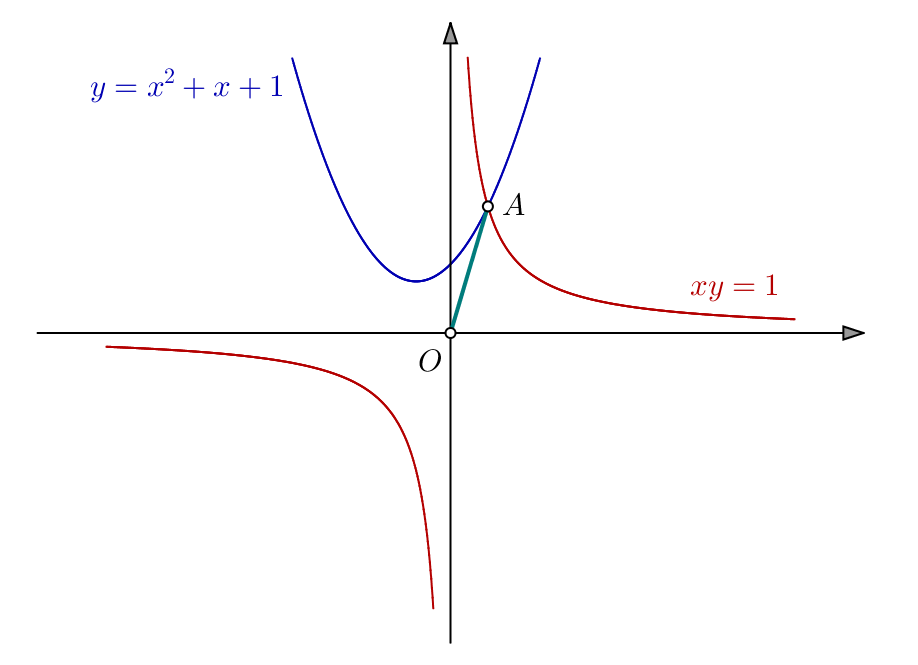
Posons, pour tout ![]() :
:
![]()
![]()
Tout d’abord :
![]()
Ainsi, la fonction ![]() est strictement croissante.
est strictement croissante.
Comme ![]() et
et ![]() le théorème des valeurs intermédiaires montre que l’équation
le théorème des valeurs intermédiaires montre que l’équation ![]() possède une unique solution
possède une unique solution ![]()
En outre :
![]()
Maintenant, on observe que :
![]()
![]()
Remarque
Le principal intérêt de cette preuve est l’absence de calcul fastidieux. Si l’on tolère une dose plus élevée de calculs, on peut tout simplement constater (à la main ou plus raisonnablement avec un outil de calcul électronique) que :
![]()
![]()
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
