icone-challenge-math-OS

Cet exercice fait l’objet d’une vidéo sur la chaine du blog Math-OS.

Peut-être préférez-vous la visionner plutôt que de lire le texte ci-dessous 🙂

Solution pour le challenge 9

Posons p=2q+1, avec q\in\mathbb{N}.

Alors, pour tout n\geqslant1 :

\displaystyle{2\,S_{n}=\sum_{k=1}^{n}\,\left(k^{2q+1}+\left(n+1-k\right)^{2q+1}\right)}

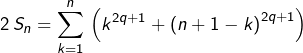
Or, pour tout \left(a,b\right)\in\mathbb{R}^{2} :

a^{2q+1}+b^{2q+1}=
\displaystyle{\left(a+b\right)\,\sum_{i=0}^{2q}\,\left(-1\right)^{i}a^{i}\,b^{2q-i}}

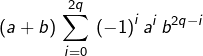
Donc, pour tout k\in\llbracket1,\cdots,n\rrbracket, l’entier k^{2q+1}+\left(n+1-k\right)^{2q+1} est multiple de k+\left(n+1-k\right)=n+1. Ainsi :

(1)   \[\boxed{n+1\mid2\,S_{n}}\]

Il s’ensuit que, si n\geqslant2, alors n\mid2S_{n-1}.

Or 2S_{n}=2S_{n-1}+2n^{2q+1} et donc :

(2)   \[\boxed{n\mid2S_{n}}\]

ce qui est encore vrai pour n=1.

D’après (1) et (2) et vu que n et n+1 sont premiers entre eux, on voit que :

    \[n\left(n+1\right)\mid2\,S_{n}\]

Enfin, l’entier n\left(n+1\right) étant pair, on peut écrire cette dernière relation sous la forme :

    \[\boxed{\frac{n\left(n+1\right)}{2}\mid S_{n}}\]

Pour consulter l’énoncé, c’est ici

Partager cet article
1   

Laisser un commentaire