Solution pour le challenge n° 81

Solution pour le challenge 81

Proposons deux méthodes.

Solution 1

L’inégalité de Cauchy-Schwarz (un cas particulier de celle-ci, en fait) dit que pour tout quadruplet $\left(u_{1},u_{2},v_{1},v_{2}\right)$ de réels :

$\left(u_{1}v_{1}+u_{2}v_{2}\right)^{2}\leqslant\left(u_{1}^{2}+u_{2}^{2}\right)\left(v_{1}^{2}+v_{2}^{2}\right)$

En choisissant $u_{1}=u_{2}=1,$ $v_{1}=a\sqrt{b}$ et $v_{2}=b\sqrt{a},$ il vient :

$\left(a\sqrt{b}+b\sqrt{a}\right)^{2}\leqslant2\left(a^{2}b+ab^{2}\right)=2ab\left(a+b\right)$

On compare alors $2ab\left(a+b\right)$ et ${\displaystyle \left[\frac{\left(a+b\right)^{2}}{2}+\frac{a+b}{4}\right]^{2}},$ c’est-à-dire $2ab$ et $\left(a+b\right)\left[\frac{a+b}{2}+\frac{1}{4}\right]^{2}$ ou encore $32ab$ et $\left(a+b\right)\left[2\left(a+b\right)+1\right]^{2}.$ Posons donc :

$\delta=\left(a+b\right)\left[2\left(a+b\right)+1\right]^{2}-32ab$

On calcule :

$\begin{eqnarray*}\delta & = & 4a^{3}+12a^{2}b+12ab^{2}+4b^{3}+4a^{2}-24ab+4b^{2}+a+b\\& = & 4\left(a+b\right)^{3}+4\left(a^{2}-6ab+b^{2}\right)+a+b\end{eqnarray*}$

Or $a^{2}-6ab+b^{2}=\left(a-b\right)^{2}-4ab$ et $4ab\leqslant\left(a+b\right)^{2};$ donc :

$\delta\geqslant\underbrace{4\left(a+b\right)^{3}-4\left(a+b\right)^{2}+\left(a+b\right)}_{=T}+4\left(a-b\right)^{2}$

et en posant $x=a+b\geqslant0$ :

$T=x\left(4x^{2}-4x+1\right)=x\left(2x-1\right)^{2}\geqslant0$

d’où la conclusion $\delta\geqslant0,$ c’est-à-dire :

$a\sqrt{b}+b\sqrt{a}\leqslant\frac{\left(a+b\right)^{2}}{2}+\frac{a+b}{4}$

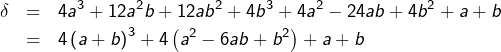
Solution 2

On passe en coordonnées polaires ! Si l’on pose $\sqrt{a}=r\cos\theta$ et $\sqrt{b}=r\sin\left(\theta\right)$ avec $r>0$ et $\theta\in\left]0,\frac{\pi}{2}\right[,$ il s’agit de montrer que :

$r^{3}\left(\sin^{2}\left(\theta\right)\cos\left(\theta\right)+\sin\left(\theta\right)\cos^{2}\left(\theta\right)\right)\leqslant\frac{r^{4}}{2}+\frac{r^{2}}{4}$

ou encore :

$2r^{2}-4r\sin\left(\theta\right)\cos\left(\theta\right)\left(\sin\left(\theta\right)+\cos\left(\theta\right)\right)+1\geqslant0$

Or :

$4\sin\left(\theta\right)\cos\left(\theta\right)\left(\sin\left(\theta\right)+\cos\left(\theta\right)\right)=2\sqrt{2}\sin\left(2\theta\right)\sin\left(\theta+\frac{\pi}{4}\right)\leqslant2\sqrt{2}$

et donc :

$2r^{2}-4r\sin\left(\theta\right)\cos\left(\theta\right)\left(\sin\left(\theta\right)+\cos\left(\theta\right)\right)+1\geqslant2r^{2}-2r\sqrt{2}+1=\left(r\sqrt{2}-1\right)^{2}\geqslant0.$

Pour consulter l’énoncé, c’est ici

Partager cet article

Solution 1

Solution 2

Laisser un commentaire Annuler la réponse