Solution pour le challenge 78
Comme 
alors 
donc 
d’après le petit théorème de Fermat.
Par ailleurs :
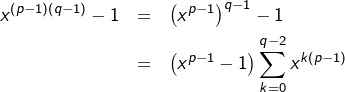
Et par transitivité : 
On voit de même que 
Et comme 
alors :
![\[\fcolorbox{black}{myBlue}{$\displaystyle{pq\mid x^{\left(p-1\right)\left(q-1\right)}-1}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-479e64deba7790a655334dad20d765e8_l3.png "Rendered by QuickLaTeX.com")
Pour consulter l’énoncé, c’est ici
Solution pour le challenge 78
Comme alors donc d’après le petit théorème de Fermat.
Par ailleurs :
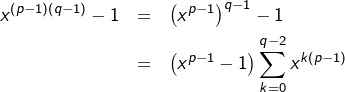
Et par transitivité :
On voit de même que
Et comme alors :
Pour consulter l’énoncé, c’est ici