Solution pour le challenge n° 72

Solution pour le challenge 72

Pour le premier point …

Il s’agit de déterminer les entiers $n\in\mathbb{N}$ pour lesquels

$R_{n}=\frac{\left(n+1\right)\left(2n+1\right)}{6}$

est entier. Comme $6=2\times3$ et vu que 2 et 3 sont premiers entre eux, cette condition équivaut à :

$\left\{\begin{array}{ccc}2\mid\left(n+1\right)\left(2n+1\right) & & \left(\alpha\right)\\\text{et}\\3\mid\left(n+1\right)\left(2n+1\right) & & \left(\beta\right)\end{array}\right.$

Comme $2n+1$ est impair, alors d’après Gauss : $\left(\alpha\right)\Leftrightarrow2\mid n+1.$ Autrement dit, $\left(\alpha\right)$ signifie que $n$ est impair.

Par ailleurs, comme $3$ est premier, on voit avec le lemme d’Euclide que $\left(\beta\right)$ équivaut à :

$3\mid n+1\qquad\text{ou}\qquad3\mid2n+1$

Les entiers $n\in\mathbb{N}$ pour lesquels $R_{n}$ est entier sont donc :

d’une part, les nombres impairs de la forme 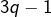$3q-1$ (ce qui impose : 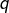$q$ pair). Ce sont les :
$\boxed{6k-1\qquad\text{avec }k\in\mathbb{N}^{\star}}$
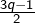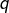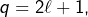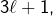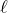d’autre part, les nombres impairs de la forme $\frac{3q-1}{2}$ (ce qui impose : $q$ impair). En posant $q=2\ell+1,$ on voit que ce sont les $3\ell+1,$ avec $\ell$ nécessairement pair. Ce sont donc les :
$\boxed{6k+1\qquad\text{avec }k\in\mathbb{N}}$

Pour le second point …

On sait que, pour tout $n\in\mathbb{N}^{\star}$ :

$\sum_{k=1}^{n}k^{2}=\frac{n\left(n+1\right)\left(2n+1\right)}{6}$

Autrement dit :

$X_{n}=\frac{\left(n+1\right)\left(2n+1\right)}{6}$

On s’intéresse donc aux couples $\left(n,y\right)\in\mathbb{N}^{2}$ pour lesquels :

$\left(n+1\right)\left(2n+1\right)=6y^{2}$

Cette équation diophantienne peut s’écrire sous la forme :

$\left(4n+3\right)^{2}-48y^{2}=1$

Notre problème se ramène donc au suivant :

Reformulation

Trouver les $\left(x,y\right)\in\mathbb{N}^{2}$ solutions de l’équation de Pell :

( $\spadesuit$ ) $x^{2}-48y^{2}=1$

pour lesquels $x\equiv3\pmod{4}$ .

Une technique classique (connue sous le nom de méthode Chakravala, qui remonte aux mathématiques indiennes des VI-ème et VII-ème siècles, voir cet article), repose sur le lemme suivant :

Identité de Brahmagupta

Quels que soient les entiers $a_{1},b_{1},a_{2},b_{2}$ et $n$ :

$\left(a_{1}^{2}-nb_{1}^{2}\right)\left(a_{2}^{2}-nb_{2}^{2}\right)=\left(a_{1}a_{2}+nb_{1}b_{2}\right)^{2}-n\left(a_{1}b_{2}+b_{1}a_{2}\right)^{2}$

Une conséquence immédiate de ce lemme est que, si l’on pose :

$\left(a_{1},a_{2}\right)\star\left(b_{1},b_{2}\right)=\left(a_{1}a_{2}+nb_{1}b_{2},\thinspace a_{1}b_{2}+b_{1}a_{2}\right)$

alors le fait que $\left(a_{1},a_{2}\right)$ et $\left(b_{1},b_{2}\right)$ soient solutions de l’équation $x^{2}-ny^{2}=1$ entraîne qu’il en va de même pour $\left(a_{1},a_{2}\right)\star\left(b_{1},b_{2}\right).$

Revenons à notre contexte …

$\left(7,1\right)$ est solution de $\left(\spadesuit\right);$ donc, si $\left(x,y\right)$ est solution de $\left(\spadesuit\right),$ alors c’est aussi le cas de :

( $\diamond$ ) $\begin{eqnarray*}\left(7,1\right)\star\left(x,y\right) & = & \left(7x+48y,x+7y\right)\end{eqnarray*}$

On produit ainsi une infinité de couples solutions de $\left(\spadesuit\right)$ .

Maintenant, il nous faut des couples solutions $\left(x,y\right)$ pour lesquels $x$ soit de la forme $4k+3.$ Or, il se trouve que, en partant de $\left(7,1\right)$ et en formant la suite des couples
$\left(x_{n},y_{n}\right)$ définis en itérant la formule $\left(\diamond\right),$ on trouve de tels couples une fois sur deux.