Solution pour le challenge 68
Considérons trois réels ![]() et l’application
et l’application ![]() définie par :
définie par :
![]()
![]()
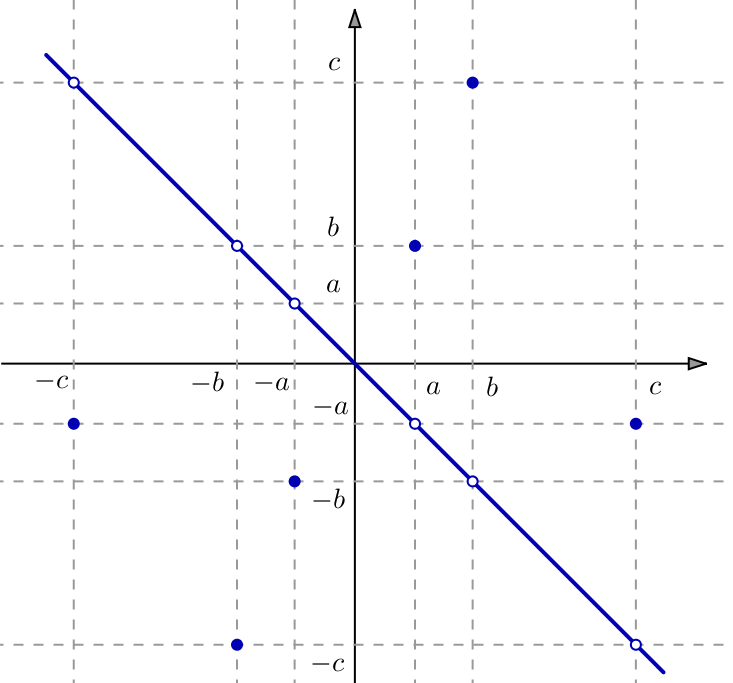
Le graphe de ![]() est représenté ci-dessous (les disques bleus indiquent des points appartennant au graphe, les disques blancs bordés de bleu indiquent des points ne lui appartenant pas) :
est représenté ci-dessous (les disques bleus indiquent des points appartennant au graphe, les disques blancs bordés de bleu indiquent des points ne lui appartenant pas) :
Considérons maintenant ![]() telle que
telle que ![]() soit strictement décroissante. Voici deux conditions qui, ajoutées à cette hypothèse, vont entraîner la décroissance stricte de
soit strictement décroissante. Voici deux conditions qui, ajoutées à cette hypothèse, vont entraîner la décroissance stricte de ![]() :
:
Condition 1 : la continuité.
En effet, comme ![]() est strictement décroissante, elle est injective, ce qui impose à
est strictement décroissante, elle est injective, ce qui impose à ![]() d’être injective. D’après un théorème classique,
d’être injective. D’après un théorème classique, ![]() est alors strictement monotone puisque continue et injective. Si
est alors strictement monotone puisque continue et injective. Si ![]() était strictement croissante, ce serait aussi le cas de
était strictement croissante, ce serait aussi le cas de ![]() Par conséquent,
Par conséquent, ![]() est strictement décroissante.
est strictement décroissante.
Condition 2 : le fait que ![]() soit croissante (au sens large).
soit croissante (au sens large).
En effet, supposons ![]() non strictement décroissante. Il existerait
non strictement décroissante. Il existerait ![]() tels que :
tels que :
![]()
![]()
Pour consulter l’énoncé, c’est ici

