icone-challenge-math-OS

Solution pour le challenge 67

On peut raisonner par homogénéïté, ce qui va réduire la complexité de la question posée.

Plus précisément, si l’on prouve que, pour tout couple \left(u,v\right) de réels strictement positifs :

(\star)   \[\left(1+u\right)\left(1+v\right)\geqslant2\sqrt{uv\left(1+u+v\right)}\]

alors l’inégalité demandée en résultera en remplaçant u et v par \frac{b}{a} et \frac{c}{a} respectivement.

Or :

    \begin{equation*}\begin{split}& \left(1+u\right)^{2}\left(1+v\right)^{2}-4uv\left(1+u+v\right)\\& = \left(1+2u+u^{2}\right)\left(1+2v+v^{2}\right)-4uv-4u^{2}v-4uv^{2}\\& = 1+2u+2v+u^{2}+v^{2}+u^{2}v^{2}-2u^{2}v-2uv^{2}\\& = \left(1+u+v-uv\right)^{2}\\& \geqslant 0\end{split}\end{equation*}

ce qui prouve \left(\star\right).

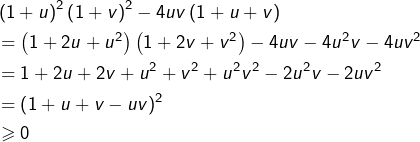
Voici maintenant une preuve plus géométrique (et aussi plus « savante ») :

On sait (formule de Héron) que l’aire d’un triangle XYZ de côtés x,y,z>0 est donnée par :

    \[\mathcal{A}=\sqrt{p\left(p-x\right)\left(p-y\right)\left(p-z\right)}\]

où p désigne le demi-périmètre :

    \[p=\frac{x+y+z}{2}\]

Par ailleurs, on sait aussi que :

    \[\mathcal{A}=\frac{1}{2}yz\sin\left(\alpha\right)\]

où \alpha\in\left]0,\pi\right[ mesure l’angle en X. Il est donc clair que :

(\diamondsuit)   \[\sqrt{p\left(p-x\right)\left(p-y\right)\left(p-z\right)}\leqslant\frac{yz}{2}\]

Considérons maintenant a,b,c>0 et posons :

    \[x=\frac{b+c}{2},\quad y=\frac{c+a}{2},\quad z=\frac{a+b}{2}\]

Il est clair que :

    \[x<y+z,\quad y<x+z,\quad\text{et }z<x+y\]

ce qui prouve que x,y,z sont les longueurs des côtés d’un triangle. En notant p son demi-périmètre, on constate que :

    \[p=\frac{a+b+c}{2},\quad p-x=\frac{a}{2},\quad p-y=\frac{b}{2},\quad p-z=\frac{c}{2}\]

et l’inégalité \left(\diamondsuit\right) prend donc la forme :

    \[2\sqrt{abc\left(a+b+c\right)}\leqslant\left(a+b\right)\left(a+c\right)\]

Pour consulter l’énoncé, c’est ici

Partager cet article
    

Laisser un commentaire