Notons ![]() le centre de
le centre de ![]()
S’il existe deux points distincts ![]() tels que
tels que ![]() soit l’orthocentre de
soit l’orthocentre de ![]() alors en notant
alors en notant ![]() l’isobarycentre :
l’isobarycentre :
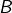 et
et 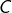 appartiennent à une perpendiculaire à
appartiennent à une perpendiculaire à 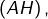
- le milieu
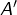 de
de ![Rendered by QuickLaTeX.com \left[B,C\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-df381c47dbf68a382968510c5844f1e6_l3.png) vérifie
vérifie 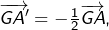
- les points
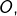
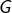 et
et 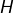 vérifient :
vérifient : 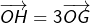 .
.
On commence donc par construire le point ![]() tel que
tel que ![]() puis le point
puis le point ![]() tel que
tel que ![]()
Si la perpendiculaire ![]() à
à ![]() passant par
passant par ![]() ne coupe pas
ne coupe pas ![]() ou bien est tangente à
ou bien est tangente à ![]() alors il
alors il
n’existe pas de solution.
Sinon, on note ![]() et l’on prouve que
et l’on prouve que ![]() est bien l’orthocentre de
est bien l’orthocentre de ![]() Pour cela, on observe que :
Pour cela, on observe que :
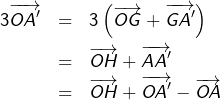
(![]() )
) ![]()
Ajoutons que, ![]() et
et ![]() étant donnés, les points
étant donnés, les points ![]() qui rendent la construction possible sont ceux pour lesquels
qui rendent la construction possible sont ceux pour lesquels ![]() est le milieu d’une corde. Or ceci revient à dire que
est le milieu d’une corde. Or ceci revient à dire que ![]() est intérieur à
est intérieur à ![]() ou encore (d’après
ou encore (d’après ![]() et en notant
et en notant ![]() le rayon de
le rayon de ![]() que
que ![]()
Le point ![]() doit donc appartenir au disque ouvert de centre
doit donc appartenir au disque ouvert de centre ![]() et de rayon
et de rayon ![]()
Illustration dynamique
Données initiales : le cercle ![]() et son centre
et son centre ![]() , ainsi que les points
, ainsi que les points ![]() et
et ![]() .
.
Les deux boutons permettent d’avancer ou de reculer d’une étape dans la construction.
En approchant le curseur suffisamment près de ![]() , de
, de ![]() ou de
ou de ![]() , un petit cercle apparaît, montrant que le point est devenu actif. On peut alors le déplacer en maintenant la touche SHIFT enfoncée et en déplaçant le curseur.
, un petit cercle apparaît, montrant que le point est devenu actif. On peut alors le déplacer en maintenant la touche SHIFT enfoncée et en déplaçant le curseur.
Pour consulter l’énoncé, c’est ici


Il me semble que le symétrique de A par rapport à H n’a aucune raison, en général, d’appartenir au cercle circonscrit Γ.
Sur la figure interactive ci-dessus (étape 5), c’est assez convaincant (quitte à déplacer un peu H).
Il est en revanche vrai que le symétrique de H par rapport au milieu A’ de [BC] appartient à Γ.
Il est aussi vrai que le symétrique orthogonal de H par rapport à la droite (BC) appartient à Γ.
Peut-être faisiez-vous plutôt référence à ces propriétés-là ? Je précise qu’elles sont inconnues d’élèves sortant du lycée (dans l’immense majorité des cas au moins).
Le symétrique A » de A par rapport à H appartient au cercle circonscrit au triangle ABC. La médiatrice de HA » coupe le cercle aux points B et C.
Cette propriété est-elle connue des élèves de 2024 ?