Solution pour le challenge n° 63

Solution pour le challenge 63

Nous allons prouver l’équivalence des assertions :

(1) $\fcolorbox{wpGray}{wpGray}{$\displaystyle{\lim_{n\rightarrow\infty}\left(x_{n+1}-x_{n}\right)=0}$}$

(2) $\fcolorbox{wpGray}{wpGray}{$K\subset F$}$

$\boxed{\left(1\right)\Rightarrow\left(2\right)}$

Soit $\lambda$ une valeur d’adhérence de la suite $\left(x_{n}\right)_{n\in\mathbb{N}}$ et soit $\varphi:\mathbb{N}\rightarrow\mathbb{N}$ strictement croissante telle que $\lim_{n\rightarrow\infty}x_{\varphi\left(n\right)}=\lambda.$

Comme $f$ est continue, alors ${\displaystyle \lim_{n\rightarrow\infty}f\left(x_{\varphi\left(n\right)}\right)=f\left(\lambda\right)},$ c’est-à-dire $\lim_{n\rightarrow\infty}x_{\varphi\left(n\right)+1}=f\left(\lambda\right).$

On voit alors que :

$\fcolorbox{wpGray}{wpGray}{$\displaystyle{f\left(\lambda\right)-\lambda=\lim_{n\rightarrow\infty}\left(x_{\varphi\left(n\right)+1}-x_{\varphi\left(n\right)}\right)=0}$}$

La dernière égalité résulte de $\left(1\right)$ et du fait que si une suite réelle converge alors toute suite extraite de celle-ci converge aussi et vers la même limite. Finalement $\lambda$ est un point fixe de $f.$

$\boxed{\left(2\right)\Rightarrow\left(1\right)}$

Si $A\subset\mathbb{R}$ , $A\neq\emptyset$ et si $t\in\mathbb{R},$ on note classiquement $d\left(t,A\right)$ la distance de $t$ à $A,$ définie par :

$\fcolorbox{black}{myBlue}{$\displaystyle{d\left(t,A\right)=\inf_{a\in A}\left|t-a\right|}$}$

On rappelle que :

L’application 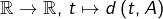$\mathbb{R}\rightarrow\mathbb{R},\thinspace t\mapsto d\left(t,A\right)$ est 1-lipschitzienne, donc continue.
Si 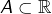$A\subset\mathbb{R}$ est un compact non vide, alors la distance à 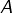$A$ est atteinte, ce qui signifie que pour tout 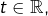$t\in\mathbb{R},$ il existe 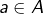$a\in A$ vérifiant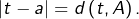 $\left|t-a\right|=d\left(t,A\right).$
L’ensemble des valeurs d’adhérence d’une quelconque suite réelle est fermé. Par conséquent, comme 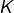$K$ est borné (puisque contenu dans $\left[0,1\right]),$ c’est un compact.

Cela dit, nous allons utiliser un petit …

Lemme

$\lim_{n\rightarrow\infty}d\left(x_{n},K\right)=0$

Preuve du lemme (cliquer pour déplier / replier)

Supposons le contraire. Il existe $\epsilon>0$ tel que, pour tout $N\in\mathbb{N},$ on peut trouver un indice $n\geqslant N$ vérifiant $d\left(x_{n},K\right)>\epsilon.$ On peut alors, par récurrence, construire une suite extraite $\left(x_{\varphi\left(n\right)}\right)_{n\in\mathbb{N}}$ telle que :

$\forall n\in\mathbb{N},\thinspace d\left(x_{\varphi\left(n\right)},K\right)>\epsilon$

La suite $\left(x_{\varphi\left(n\right)}\right)_{n\in\mathbb{N}}$ étant bornée (elle est à termes dans $\left[0,1\right]),$ elle possède (théorème de Bolzano-Weierstrass) une suite extraite convergente $\left(x_{\varphi\circ\psi\left(n\right)}\right)_{n\in\mathbb{N}},$ dont la limite est notée $\mu.$ Evidemment, $\mu\in K.$

Pourtant, en passant à la limite dans l’inégalité $d\left(x_{\varphi\circ\psi\left(n\right)},K\right)>\epsilon$ et compte tenu de la continuité de $t\mapsto d\left(t,K\right),$ on voit que $d\left(\mu,K\right)\geqslant\epsilon.$ En particulier $d\left(\mu,K\right)\neq0,$ ce qui signifie que $\mu$ n’appartient pas à l’adhérence de $K,$ autrement dit que $\mu\notin K$ (puisque $K$ est fermé). Contradiction !

Passons à la preuve de l’implication $\left(2\right)\Rightarrow\left(1\right)$ proprement dite.

Pour tout $n\in\mathbb{N},$ il existe une valeur d’adhérence $\lambda_{n}$ telle que $d\left(x_{n},K\right)=\left|x_{n}-\lambda_{n}\right|$ (ce qui résulte, comme rappelé plus haut, de la compacité de $K).$

On observe que :
$x_{n+1}-x_{n}=f\left(x_{n}\right)-x_{n}$
$=\left[f\left(x_{n}\right)-f\left(\lambda_{n}\right)\right]+\left[f\left(\lambda_{n}\right)-\lambda_{n}\right]+\left[\lambda_{n}-x_{n}\right]$
D’après le lemme : $\lim_{n\rightarrow\infty}\left(x_{n}-\lambda_{n}\right)=0$ et donc, vu que $f$ est uniformément continue (d’après le théorème de Heine), $\lim_{n\rightarrow\infty}\left(f\left(x_{n}\right)-f\left(\lambda_{n}\right)\right)=0.$