Solution pour le challenge 59
Considérons l’application ![]() définie par :
définie par :
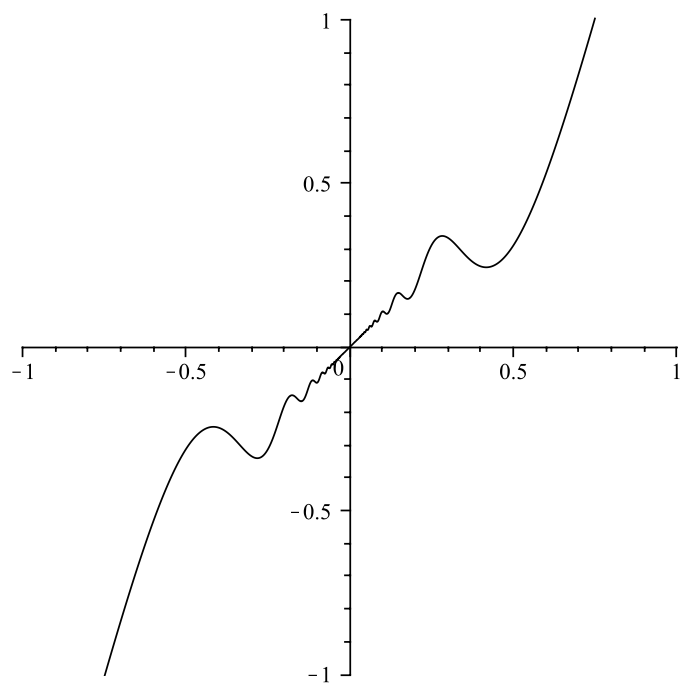
![Rendered by QuickLaTeX.com \[f(x)=\left\{ \begin{array}{cc}x^{2}\sin\left(\frac{2}{x}\right)+x & \text{si }x\neq0\\\\0 & \text{si }x=0\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9a0ac76168b9ca8d17aac9be702dcef0_l3.png)
Si l’on pose pour tout ![]() :
:
![]()
![]()
Ceci montre que ![]() est dérivable en
est dérivable en ![]() et que
et que ![]()
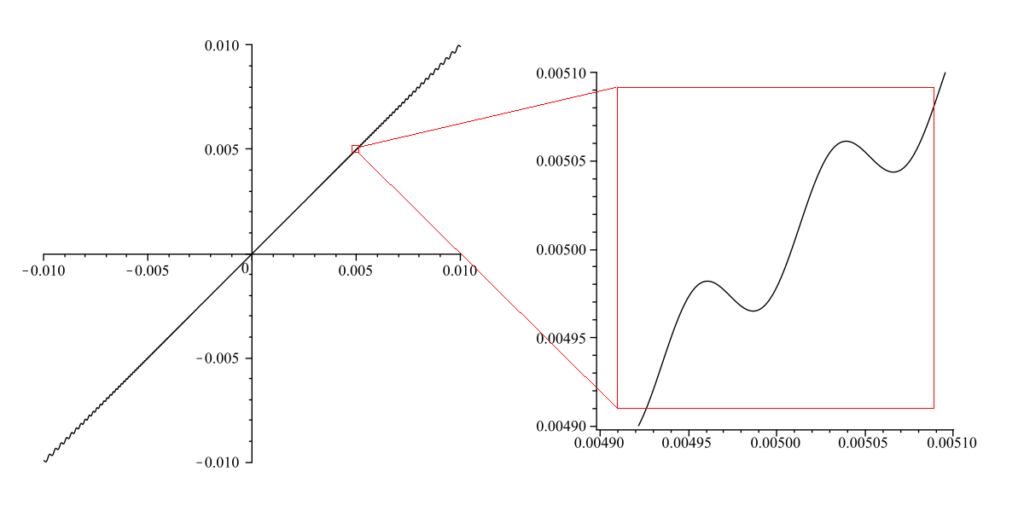
Maintenant, vérifions que ![]() n’est monotone sur aucun intervalle de la forme
n’est monotone sur aucun intervalle de la forme ![]() pour
pour ![]() Pour tout
Pour tout ![]() :
: ![]()
On observe que ![]() et que pour tout
et que pour tout ![]() la quantité
la quantité ![]() prend sur
prend sur ![]() toutes les valeurs comprises entre -1 et 3.
toutes les valeurs comprises entre -1 et 3.
Ainsi, pour tout ![]()
![]() prend sur l’intervalle
prend sur l’intervalle ![]() des valeurs strictement positives et des valeurs strictement négatives. Et comme
des valeurs strictement positives et des valeurs strictement négatives. Et comme ![]() est continue sur un tel intervalle, cela entraîne qu’il existe des sous-intervalles de
est continue sur un tel intervalle, cela entraîne qu’il existe des sous-intervalles de ![]() sur lesquels
sur lesquels ![]() est strictement croissante et d’autres sur lesquels elle est strictement décroissante.
est strictement croissante et d’autres sur lesquels elle est strictement décroissante.
Pour consulter l’énoncé, c’est ici

