icone-challenge-math-OS

Solution pour le challenge 58

Vue la symétrie de l’expression, on peut se limiter aux couples \left(p,q\right)\in\mathbb{N}^{2} pour lesquels q\geqslant p.

Nous allons prouver que si q>p\geqslant2, alors A\left(p,q\right)\leqslant A\left(p,q-1\right).

Il en résultera, par une récurrence immédiate, que :

\boxed{q>p\geqslant2\Rightarrow A\left(p,q\right)\leqslant A\left(p,p\right)} (1)

Ensuite, nous verrons que :
\boxed{p\geqslant2\Rightarrow A\left(p,p\right)\leqslant A\left(2,2\right)} (2)

En combinant (1) et (2), on pourra en déduire que :

    \[q>p\geqslant2\Rightarrow A\left(p,q\right)\leqslant\frac{4}{45}\]

Enfin, on vérifiera que :
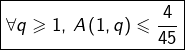\boxed{\displaystyle{\forall q\geqslant1,\thinspace A\left(1,q\right)\leqslant\frac{4}{45}}} (3)
ce qui donnera finalement :

    \[\boxed{\forall\left(p,q\right)\in\mathbb{N}^{\star2},\thinspace A\left(p,q\right)\leqslant\frac{4}{45}}\]

Autrement dit : la plus grande valeur possible pour A\left(p,q\right) est obtenue pour p=q=2. Détaillons maintenant les calculs.

Preuve détaillée de (1)

Avant tout, on a pour tout \left(p,q\right)\in\mathbb{N}^{\star} : \displaystyle{A\left(p,q\right)=\frac{pq}{\left(p+1\right)\left(q+1\right)\left(p+q+1\right)}}

Supposons q>p\geqslant2; alors (en notant \# pour du même signe que ) :

    \begin{eqnarray*}&&A\left(p,q-1\right)-A\left(p,q\right)\\& = & \frac{p\left(q-1\right)}{\left(p+1\right)q\left(p+q\right)}\\& &-\frac{pq}{\left(p+1\right)\left(q+1\right)\left(p+q+1\right)}\\ & \# & \frac{q-1}{q\left(p+q\right)}\\& &-\frac{q}{\left(q+1\right)\left(p+q+1\right)}\\ & \# & \left(q^{2}-1\right)\left(p+q+1\right)\\& &-q^{2}\left(p+q\right)\\ & = & q^{2}-p-q-1 \end{eqnarray*}

Or q^{2}-q>p^{2}-p car q^{2}-q-\left(p^{2}-p\right)=\left(q-p\right)\left(p+q-1\right)>0. Donc :

    \begin{eqnarray*}& &A\left(p,q-1\right)-A\left(p,q\right)\\& > & p^{2}-2p-1\\&=&\left(p-1\right)^{2}-2\\&\geqslant&-1\end{eqnarray*}

ce qui prouve que :

    \[A\left(p,q-1\right)\geqslant A\left(p,q\right).\]

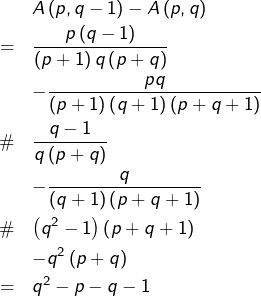
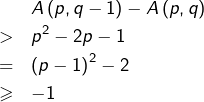
Preuve détaillée de (2)

Pour tout p\geqslant2 :

    \begin{eqnarray*}&&A\left(2,2\right)-A\left(p,p\right)\\& = & \frac{4}{45}-\frac{p^{2}}{\left(p+1\right)^{2}\left(2p+1\right)}\\ & \# & 4\left(p+1\right)^{2}\left(2p+1\right)-45p^{2}\\ & = & 8p^{3}-25p^{2}+16p+4\\ & = & \left(p-2\right)\left(8p^{2}-9p-2\right) \end{eqnarray*}

Or le trinôme 8p^{2}-9p-2 admet pour plus grande racine :

    \[\lambda=\frac{9+\sqrt{145}}{16}\simeq1,31\]

On a donc bien A\left(2,2\right)-A\left(p,p\right)\geqslant0 pour tout p\geqslant2.

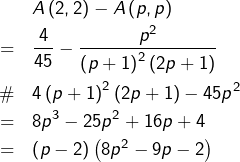
Preuve détaillée de (3)

Pour tout q\geqslant1 :

    \begin{eqnarray*}&&\frac{4}{45}-A\left(1,q\right)\\& = & \frac{4}{45}-\frac{q}{2\left(q+1\right)\left(q+2\right)}\\ & \# & 8\left(q+1\right)\left(q+2\right)-45q\\ & = & 8q^{2}-21q+16 \end{eqnarray*}

Or, le discriminant de ce dernier trinôme est \Delta=441-512<0.

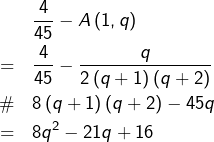
On a donc bien 8q^{2}-21q+16>0.

Pour consulter l’énoncé, c’est ici

Partager cet article
    

Laisser un commentaire