Solution pour le challenge n° 57

Solution pour le challenge 57

Comme $n$ est supposé impair, la condition $1+\omega^{k}\neq0$ est remplie pour entier $k.$

Détail pour cette affirmation (cliquer pour déplier / replier)

Pour qu’on ait $\omega^{k}=-1,$ c’est-à-dire $e^{2ik\pi/n}=e^{i\pi},$ il faudrait que $\frac{2k\pi}{n}=\pi+2q\pi$ pour un certain entier $q,$ ce qui imposerait $2k=n\left(2q+1\right).$ Or ceci est impossible (égalité entre deux entiers de parités contraires).

La somme

$S_{n}=\sum_{k=0}^{n-1}\frac{1}{\left(1+\omega^{k}\right)^{2}}$

est donc bien définie.

Rappelons que, pour tout polynôme $P$ scindé dans $\mathbb{C}\left[X\right]$ et à racines simples, en posant $P=a\prod\limits_{k=1}^{n}\left(X-\alpha_{k}\right)$ avec $a\neq0$ et les $\alpha_{k}$ deux à deux distincts, on la formule :

$\sum_{k=1}^{n}\frac{1}{X-\alpha_{k}}=\frac{P'}{P}$

En appliquant ceci à $P=X^{n}-1$ , et vu que $P=\prod\limits _{k=0}^{n-1}(X-\omega^{k})$ , on obtient :

$\sum_{k=0}^{n-1}\frac{1}{X-\omega^{k}}=\frac{nX^{n-1}}{X^{n}-1}$

Après dérivation et changement de signe, on obtient : 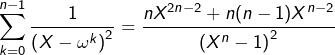$\displaystyle{\sum_{k=0}^{n-1}\frac{1}{\left(X-\omega^{k}\right)^{2}}=\frac{nX^{2n-2}+n(n-1)X^{n-2}}{\left(X^{n}-1\right)^{2}}}$

Il ne reste plus qu’à évaluer en -1 (sans oublier que $n$ est impair) pour obtenir :

$\boxed{\sum_{k=0}^{n-1}\frac{1}{(1+\omega^{k})^{2}}=\frac{n\left(2-n\right)}{4}}$

Pour consulter l’énoncé, c’est ici

Partager cet article

Laisser un commentaire Annuler la réponse