Solution pour le challenge 56
En posant :
![]()
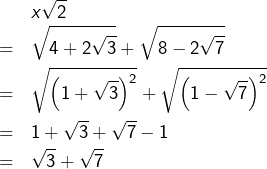
d’où :
![]()
![]()
Proposition
Pour tout ![]() :
:
![]()
![]()
Pour consulter l’énoncé, c’est ici
Solution pour le challenge 56
En posant :
![]()
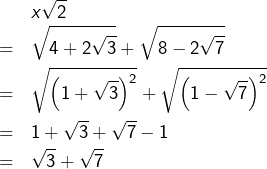
![]()
![]()
Pour tout ![]() :
:
![]()
![]()
Pour consulter l’énoncé, c’est ici