icone-challenge-math-OS

Solution pour le challenge 55

Rappelons avant tout un résultat ultra-classique :

Lemme

Pour tout x\in\left]-1,+\infty\right[ :

    \[\ln\left(x+1\right)\leqslant x\qquad\left(\star\right)\]

Ceci se prouve aisément en étudiant les variations de \varphi:x\mapsto x-\ln\left(x+1\right).

En effet, \varphi est dérivable et sa dérivée est donnée par :

    \[\varphi'\left(x\right)=1-\frac{1}{x+1}=\frac{x}{x+1}\]

Cette dernière expression est du signe de x (car x+1>0 dans ce contexte), ce qui montre que \varphi décroît sur \left]-1,0\right] puis croît sur \left[0,+\infty\right[. De ce fait, \varphi présente un minimum en 0, qui vaut \varphi\left(0\right)=-\ln\left(1\right)=0, d’où la positivité de \varphi, ce qui prouve \left(\star\right).

On peut aussi invoquer un argument de concavité : la fonction x\mapsto\ln\left(x+1\right) est concave (car sa dérivée seconde est négative) et son graphe se situe donc au-dessous de n’importe laquelle de ses tangentes — notamment la tangente à l’origine.

Abordons à présent la question proposée.

Etudions, pour x>-1, le signe de :

    \[\boxed{f\left(x\right)=\left(x+1\right)\ln^{2}\left(x+1\right)-x^{2}}\]

Il est clair que f est deux fois (et même indéfiniment) dérivable.

On calcule successivement :
f'\left(x\right)=\ln^{2}\left(x+1\right)+2\ln\left(x+1\right)-2x
puis :
\displaystyle{f''\left(x\right)=\frac{2\ln\left(x+1\right)}{x+1}+\frac{2}{x+1}-2} \displaystyle{=\frac{2\left(\ln\left(x+1\right)-x\right)}{x+1}}

D’après le lemme, f''\left(x\right)\leqslant0 pour tout x>-1, ce qui prouve que f' est décroissante.

Comme f'\left(0\right)=0, il en résulte que f'\left(x\right)\geqslant0 pour x\in\left]-1,0\right] et f'\left(x\right)\leqslant0 pour x\geqslant0.

Ainsi, f est croissante sur \left]-1,0\right] puis décroissante sur \left[0,+\infty\right[.

Pour finir, f\left(0\right)=0 et donc f\left(x\right)\leqslant0 pour tout x>-1. Autrement dit :
\boxed{\forall x\in\left]-1,+\infty\right[,\thinspace\left(x+1\right)\ln^{2}\left(x+1\right)-x^{2}\leqslant0}

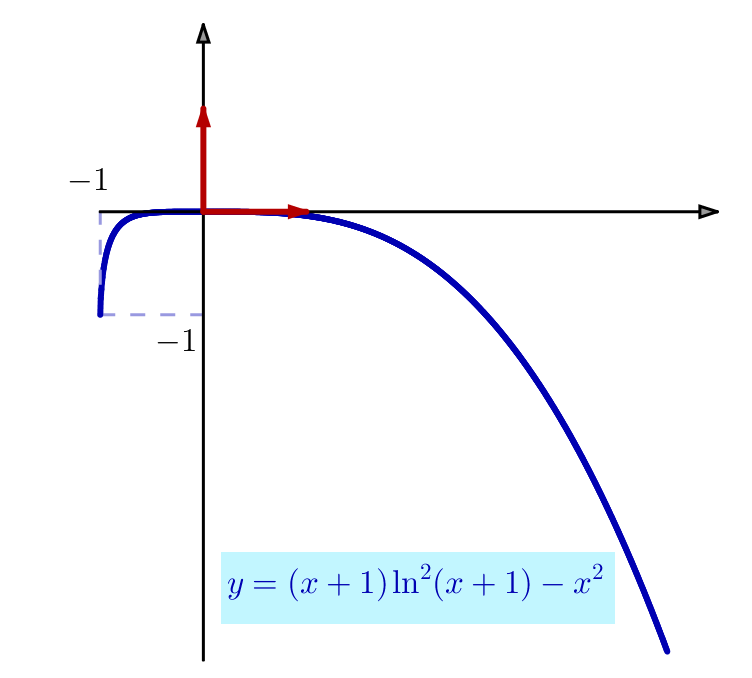
Ci-dessous, l’allure du graphe de f :

Pour consulter l’énoncé, c’est ici

Partager cet article
  •  
  •  
  •  
  •  

Laisser un commentaire