Solution pour le challenge 50
Question 1
Notons ![]() l’ensemble des mots binaires de longueur
l’ensemble des mots binaires de longueur ![]() comportant
comportant ![]() fois le symbole 1.
fois le symbole 1.
Imaginons un casier, composé de ![]() cases vides. Construire un élément de
cases vides. Construire un élément de ![]() consiste à répartir dans le casier
consiste à répartir dans le casier ![]() symboles 1 et
symboles 1 et ![]() symboles 0.
symboles 0.
Le nombre de possibilités est donc égal au nombre de façons de choisir ![]() cases parmi
cases parmi ![]() (celles destinées à accueillir le symbole 1).
(celles destinées à accueillir le symbole 1).
Ainsi, en posant ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{\alpha_{n,p}=\binom{n}{p}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-eb085696d82094247d8377aae9e2d86d_l3.png)
Question 2
Notons ![]() l’ensemble des mots binaires de longueur
l’ensemble des mots binaires de longueur ![]() ne comportant pas deux 1 consécutifs.
ne comportant pas deux 1 consécutifs.
Notons ![]() Clairement :
Clairement :
![]()
![]()
Classons les mots de longueur ![]() ne comportant pas la séquence 11 en deux catégories :
ne comportant pas la séquence 11 en deux catégories :
- ceux commençant par 0 : ils forment un sous-ensemble noté
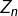 .
. - ceux commençant par 1 : ils forment un sous-ensemble noté
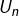
Les éléments de ![]() sont obtenus en préfixant par 0 ceux de
sont obtenus en préfixant par 0 ceux de ![]() .
.
Les éléments de ![]() sont obtenus en préfixant par 10 ceux de
sont obtenus en préfixant par 10 ceux de![]() .
.
En outre ![]() (union disjointe). En passant aux cardinaux, on en déduit :
(union disjointe). En passant aux cardinaux, on en déduit :
![]()
Finalement, pour tout ![]() :
:
![]()
Question 3
Les choses se compliquent …
Notons ![]() l’ensemble des mots binaires de longueur
l’ensemble des mots binaires de longueur ![]() comportant
comportant ![]() fois la séquence 01 et posons
fois la séquence 01 et posons ![]()
Commençons par déterminer ![]() c’est-à-dire le nombre de mots binaires de longueur
c’est-à-dire le nombre de mots binaires de longueur ![]() ne comportant pas la séquence 01.
ne comportant pas la séquence 01.
Un tel mot doit être composé, pour un certain ![]() de
de ![]() symboles 1 suivis de
symboles 1 suivis de ![]() symboles 0 (justification ci-dessous). Par conséquent :
symboles 0 (justification ci-dessous). Par conséquent :
![]()
Détail (cliquer pour déplier / replier)
Notons ![]() les lettres d’un mot binaire de longueur
les lettres d’un mot binaire de longueur ![]() ne comportant pas la séquence 01 et supposons l’existence d’un couple
ne comportant pas la séquence 01 et supposons l’existence d’un couple ![]() tel que
tel que ![]()
![]() et
et ![]() Soient alors :
Soient alors :![]()
et![]()
En clair :
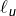 est le 0 le plus à droite tel qu’il existe un 1 à droite de cette position (pas forcément juste après),
est le 0 le plus à droite tel qu’il existe un 1 à droite de cette position (pas forcément juste après),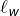 est le 1 le plus à gauche parmi les 1 situés à droite de
est le 1 le plus à gauche parmi les 1 situés à droite de 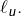
Supposons un instant que ![]() et considérons un entier
et considérons un entier ![]() tel que
tel que ![]() On ne peut avoir ni
On ne peut avoir ni ![]() (par définition de
(par définition de ![]() ) ni
) ni ![]() (par définition de
(par définition de ![]() . Donc
. Donc ![]() ce qui montre la présence de la séquence 01, contrairement à l’hypothèse.
ce qui montre la présence de la séquence 01, contrairement à l’hypothèse.
On a montré par l’absurde que, dans un mot de longueur ![]() ne comportant pas la séquence 01, on ne peut pas trouver un 0 suivi plus loin d’un 1. Ce mot est donc formé d’une séquence (éventuellement vide) de 1, suivie d’une séquence (éventuellement vide) de 0.
ne comportant pas la séquence 01, on ne peut pas trouver un 0 suivi plus loin d’un 1. Ce mot est donc formé d’une séquence (éventuellement vide) de 1, suivie d’une séquence (éventuellement vide) de 0.
Nous allons établir une bijection entre les ensembles ![]() et
et ![]() (notation de la question 1).
(notation de la question 1).
Etant donné ![]() préfixons ce mot par 1 et suffixons-le par 0.
préfixons ce mot par 1 et suffixons-le par 0.
A partir du mot ![]() obtenu (qui est de longueur
obtenu (qui est de longueur ![]() construisons un mot
construisons un mot ![]() de longueur
de longueur ![]() comme suit :
comme suit :
![]()
➡ Ceci définit une application ![]()
Par exemple, en partant de :

on forme successivement le mot :
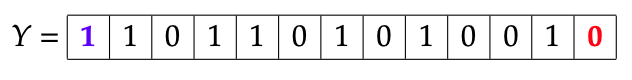
puis le mot :

Inversement, considérons un mot ![]() et construisons un mot
et construisons un mot ![]() de longueur
de longueur ![]() de la manière suivante :
de la manière suivante :![]()
et![]()
Comme ![]() comporte un nombre impair de 1, on aura un nombre impairs de « changements » dans
comporte un nombre impair de 1, on aura un nombre impairs de « changements » dans ![]() (un changement est la transition d’un 0 vers un 1 ou inversement) et en particulier
(un changement est la transition d’un 0 vers un 1 ou inversement) et en particulier ![]()
Ensuite, supprimons le 1 en tête de ![]() et le 0 en queue, autrement dit posons
et le 0 en queue, autrement dit posons ![]() avec :
avec :
![]()
Le mot ![]() est de longueur
est de longueur ![]() et comporte
et comporte ![]() fois la séquence 01 : en effet, comme
fois la séquence 01 : en effet, comme ![]() commence par un 1, le premier changement produit la séquence séquence 10 et il reste ensuite
commence par un 1, le premier changement produit la séquence séquence 10 et il reste ensuite ![]() changements : la moitié d’entre-eux donnent la séquence 01.
changements : la moitié d’entre-eux donnent la séquence 01.
➡ Ceci définit une application ![]() Or :
Or :
![]()
![]()
Ainsi ![]() c’est-à-dire :
c’est-à-dire :
![Rendered by QuickLaTeX.com \[\boxed{\gamma_{n,p}=\binom{n+1}{2p+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1cdf45ad49783a266e585fb76e2c82c7_l3.png)
Pour consulter l’énoncé, c’est ici

