Solution pour le challenge 49
![]()
Supposons ![]() infini et soit
infini et soit ![]() une application. Etant donné
une application. Etant donné ![]() , considérons la partie
, considérons la partie ![]()
Ici, ![]() désigne la
désigne la ![]() -ème itérée de
-ème itérée de ![]() c’est-à-dire
c’est-à-dire ![]()
Alors :
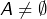 (puisque
(puisque  ).
).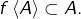 En effet, si
En effet, si 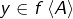 , alors il existe
, alors il existe 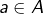 tel que
tel que 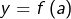 et il existe
et il existe 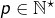 tel que
tel que 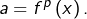 Ainsi :
Ainsi : 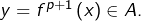
- Pour voir que
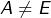 , distinguons deux cas. Si
, distinguons deux cas. Si 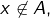 c’est clair. Sinon, il existe
c’est clair. Sinon, il existe 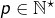 tel que
tel que 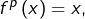 auquel cas :
auquel cas :
En effet, l’inclusion![Rendered by QuickLaTeX.com \[A=\{f^i(x);\:0\leqslant i\leqslant p-1\}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e75ef7570fe5a1c9b3c3c82d129e14d2_l3.png)
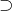 est évidente et l’inclusion inverse se voit facilement par division euclidienne. Il en résulte en particulier que
est évidente et l’inclusion inverse se voit facilement par division euclidienne. Il en résulte en particulier que 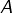 est fini et donc que
est fini et donc que 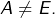
On a bien construit une partie de ![]() ayant les propriétés voulues.
ayant les propriétés voulues.
![]()
On prouve la contraposée. Supposons ![]() fini et posons
fini et posons ![]()
Soit alors ![]() définie par :
définie par :![]()
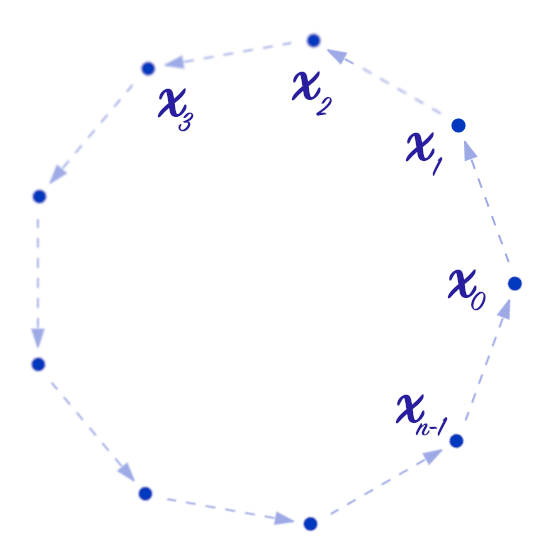
Soit ![]() une partie propre de
une partie propre de ![]() Si
Si ![]() alors
alors ![]() ce qui est exclu. Il existe donc
ce qui est exclu. Il existe donc ![]() tel que
tel que ![]() et
et ![]()
Ainsi : ![]() , comme souhaité.
, comme souhaité.
Très bonne solution proposée par Joël CHARLES-REBUFFE, futur élève en section MP* au lycée Thiers (Marseille).
Pour consulter l’énoncé, c’est ici

