icone-challenge-math-OS

Solution pour le challenge 48

Commençons par établir un résultat préliminaire.

Lemme

Il existe a\in\left]0,1\right] tel que : \forall t\in\mathbb{R},\,\left|\sin\left(t\right)\right|\leqslant a\Rightarrow\left|\sin\left(t+1\right)\right|\geqslant a

Preuve (cliquer pour déplier / replier)

L’idée intuitive est que si \sin\left(t\right) est assez proche de 0, alors \left|\sin\left(t+1\right)\right| est arbitrairement proche de \left|\sin\left(1\right)\right| donc loin de 0.

Formalisons cela : \left|\sin\left(t+1\right)\right|=\left|\sin\left(t\right)\cos\left(1\right)+\cos\left(t\right)\sin\left(1\right)\right
\geqslant\left|\cos\left(t\right)\right|\sin\left(1\right)-\left|\sin\left(t\right)\right|\cos\left(1\right) =\sqrt{1-\sin^{2}\left(t\right)}\sin\left(1\right)-\left|\sin\left(t\right)\right|\cos\left(1\right)

Donc, étant donné a\in\left]0,1\right[; si \left|\sin\left(t\right)\right|\leqslant a alors :\left|\sin\left(t+1\right)\right|\geqslant\sqrt{1-a^{2}}\sin\left(1\right)-a\cos\left(1\right)

Notons \varphi\left(a\right) cette dernière quantité.

Comme {\displaystyle \lim_{a\rightarrow0^{+}}\frac{\varphi\left(a\right)}{a}=+\infty}, on peut choisir a\in\left]0,1\right[ de telle sorte que \varphi\left(a\right)\geqslant a.

Alors, pour tout t\in\mathbb{R} : \left|\sin\left(t\right)\right|\leqslant a\Rightarrow\left|\sin\left(t+1\right)\right|\geqslant a

Cela dit, fixons p\in\mathbb{N}^{\star} ainsi que \alpha\in\left]0,1\right[ et notons, pour tout n\in\mathbb{N}^{\star} :

    \[S_{n}=\sum_{k=1}^{n}\frac{\left|\sin^{p}\left(k\right)\right|}{k^{\alpha}}\]

On va minorer S_{2n} par une quantité qui tend vers +\infty lorsque n\rightarrow+\infty, ce qui montrera la divergence de la série proposée.
En regroupant les termes deux par deux, en voit que :
\displaystyle{S_{2n}=\sum_{j=1}^{n}\left(\frac{\left|\sin^{p}\left(2j-1\right)\right|}{\left(2j-1\right)^{\alpha}}+\frac{\left|\sin^{p}\left(2j\right)\right|}{\left(2j\right)^{\alpha}}\right)}

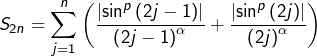
Pour tout j\in\left\llbracket 1,n\right\rrbracket et d’après le lemme, l’un au moins des deux réels \left|\sin\left(2j-1\right)\right| ou \left|\sin\left(2j\right)\right| est plus grand que a.

De ce fait, pour tout j\in\mathbb{N}^{\star} : \displaystyle{\frac{\left|\sin^{p}\left(2j-1\right)\right|}{\left(2j-1\right)^{\alpha}}+\frac{\left|\sin^{p}\left(2j\right)\right|}{\left(2j\right)^{\alpha}}\geqslant\frac{a^{p}}{\left(2j\right)^{\alpha}}}

Et donc :

    \[S_{2n}\geqslant\frac{a^{p}}{2^{\alpha}}\sum_{j=1}^{n}\frac{1}{j^{\alpha}}\]

Mais la série de Riemann {\displaystyle \sum_{j\geqslant1}\frac{1}{j^{\alpha}}} est divergente, d’où le résultat annoncé.

Pour consulter l’énoncé, c’est ici

Partager cet article
    

Laisser un commentaire