Solution pour le challenge 44
Soient ![]() des entiers tels que
des entiers tels que ![]() et
et ![]()
Notons ![]() le nombre de
le nombre de ![]() uplets
uplets ![]() d’entiers compris (au sens large) entre
d’entiers compris (au sens large) entre ![]() et
et ![]() , tels que
, tels que ![]()
En symboles :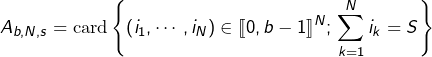
L’énoncé demande le calcul de ![]()
Le cœur de ce qui va suivre réside dans l’observation-clef suivante :
![]() est le coefficient de
est le coefficient de ![]() dans le développement du polynôme :
dans le développement du polynôme :
![Rendered by QuickLaTeX.com \[P=\left(\sum_{i=0}^{b-1}\,X^{i}\right)^{N}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a7cc5c4e95ce80f839aed072ee6fd1b0_l3.png)
Transformons maintenant l’écriture de ![]() en passant par une série formelle :
en passant par une série formelle :
![Rendered by QuickLaTeX.com \[P=\left(\frac{1-X^{b}}{1-X}\right)^{N}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1b184d5e80087ee07531c26125795abd_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{1-X}=\sum_{k=0}^{+\infty}X^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-15c92dcd5bcf075ef3949570df7f4c74_l3.png)
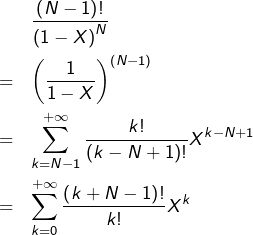
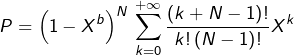
c’est-à-dire, via la formule du binôme :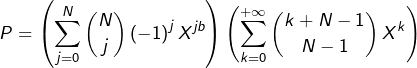
Le coefficient de ![]() dans l’expression développée de
dans l’expression développée de ![]() est donc :
est donc :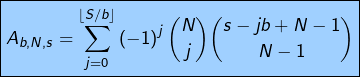
En particulier, et pour revenir au cas qui nous intéresse :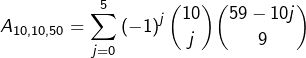
Soit, après calcul sur machine : ![]()
Tiens! C’est un nombre premier 🙂
Pour consulter l’énoncé, c’est ici

