Solution pour le challenge 42
Solution proposée par Emilien Paganelli, étudiant en section MP* au lycée Thiers, Marseille.
1 – Irrationalité de 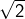
Lemme
Si ![]() est un entier naturel qui n’est pas un carré parfait, alors
est un entier naturel qui n’est pas un carré parfait, alors ![]() est irrationnel.
est irrationnel.
Il est clair que ![]() , ce qui entraîne l’existence d’une décomposition en facteurs premiers (DFP) pour
, ce qui entraîne l’existence d’une décomposition en facteurs premiers (DFP) pour ![]() . Supposons que
. Supposons que ![]() avec
avec ![]() . Alors :
. Alors : ![]() . Comme les exposants qui apparaissent dans les DFP de
. Comme les exposants qui apparaissent dans les DFP de ![]() et de
et de ![]() sont tous pairs, on voit par différence qu’il en va de même pour les exposants apparaissant dans la DFP de N. Mais ceci entraîne que N est un carré : contradiction ! Donc
sont tous pairs, on voit par différence qu’il en va de même pour les exposants apparaissant dans la DFP de N. Mais ceci entraîne que N est un carré : contradiction ! Donc ![]() .
.
En particulier, ![]() est irrationnel.
est irrationnel.
2 – Solution du challenge
Considérons le polynôme ![]() .
.
Vu que ![]() est irrationnel :
est irrationnel :
![]()
Et puisqu’un entier naturel non nul est supérieur ou égal à 1, on obtient :
![]()
![]()
Par ailleurs, d’après l’inégalité des accroissements finis :
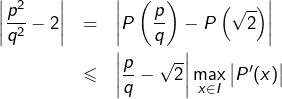
où ![]() désigne le segment d’extrémités
désigne le segment d’extrémités ![]() et
et ![]() . Donc :
. Donc :
![]()
![Rendered by QuickLaTeX.com \[\left|\frac{p^{2}}{q^{2}}-2\right|\leqslant2\left|\frac{p}{q}-\sqrt{2}\right|\max\left\{\frac{\sqrt{2}}{2}+1,\frac{p}{q}\right\}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6878f9658566010721709c99f9c6873c_l3.png)
En combinant ceci avec ![]() , il vient :
, il vient :
![Rendered by QuickLaTeX.com \[2\left|\frac{p}{q}-\sqrt{2}\right|\max\left\{\frac{\sqrt{2}}{2}+1,\frac{p}{q}\right\}\geqslant\frac{1}{q^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-461c121c7a579694aec4c8c43e3e0cf3_l3.png)
Distinguons deux cas :
- Si
![Rendered by QuickLaTeX.com \frac{p}{q}\notin[0,\frac{\sqrt{2}}{2}+1]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3be3b7e42855f2d0bb5ead138f9e9a35_l3.png) , alors :
, alors :
Ainsi :![Rendered by QuickLaTeX.com \[\left|\frac{p}{q}-\sqrt{2}\right|\geqslant1-\frac{\sqrt{2}}{2}=\frac{1}{2+\sqrt{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-40d33c8bb22db6415c5007b2d6395669_l3.png)
![Rendered by QuickLaTeX.com \[\left|\frac{p}{q}-\sqrt{2}\right|\geqslant\frac{1}{(2+\sqrt{2})q^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1d311358b9bc6db056eeee9ad91843a7_l3.png)
- Sinon
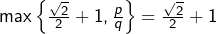 et donc :
et donc :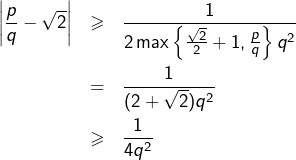
Dans tous les cas :
![]()
On a même obtenu un résultat un peu meilleur :
![Rendered by QuickLaTeX.com \[\boxed{\left|\frac{p}{q}-\sqrt{2}\right|\geqslant\frac{1}{(2+\sqrt{2})q^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5ed0307b76a48cd6ee49242964c7b5e2_l3.png)
3 – Une majoration plus fine
Notons ![]() l’unique réel strictement positif tel que
l’unique réel strictement positif tel que
![]()
![]()
Soit maintenant ![]() . Distinguons trois cas :
. Distinguons trois cas :
- Pour
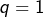 et
et 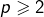 :
:![Rendered by QuickLaTeX.com \[\left|\frac{p}{q}-\sqrt{2}\right|\geqslant2-\sqrt{2}\geqslant\frac{1}{2}\geqslant\frac{1}{2xq^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-26d52b98a8b2af436c0368710b0d1bea_l3.png)
- Pour
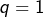 et
et 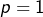 :
:![Rendered by QuickLaTeX.com \[\left|\frac{p}{q}-\sqrt{2}\right|=\sqrt{2}-1\geqslant0.41\geqslant\frac{1}{2xq^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9170b8d1d2029c90599745e654c8a14e_l3.png)
- Supposons désormais
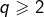 . D’après
. D’après 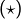 et vu que
et vu que 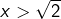 :
: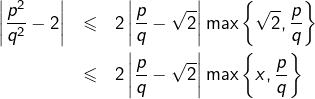
- Si
![Rendered by QuickLaTeX.com \frac{p}{q}\notin[0,x]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b229b135a7c96d535b60708104569579_l3.png) :
:![Rendered by QuickLaTeX.com \[\left|\frac{p}{q}-\sqrt{2}\right|\geqslant x-\sqrt{2}=\frac{1}{2x2^{2}}\geqslant\frac{1}{2xq^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-63e2c35b14b1badbb8ecb227d470216a_l3.png)
- Si
![Rendered by QuickLaTeX.com \frac{p}{q}\in[0,x]](https://math-os.com/wp-content/ql-cache/quicklatex.com-110f84ae39ebbb360641482679467ed9_l3.png) :
:![Rendered by QuickLaTeX.com \[\left|\frac{p}{q}-\sqrt{2}\right|\geqslant\frac{1}{2\max\left\{x,\frac{p}{q}\right\} q^{2}}=\frac{1}{2xq^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1b4be87911a0bd0a1a5ac500e90e7e24_l3.png)
- Si
Nous avons obtenu le résultat suivant :
![Rendered by QuickLaTeX.com \[\boxed{\left|\frac{p}{q}-\sqrt{2}\right|\geqslant\frac{1}{\left(\sqrt{2}+\frac{\sqrt{10}}{2}\right)q^{2}}\geqslant\frac{1}{3q^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b25114f65a6a0be391b4bd13e6058835_l3.png)
4 – Epilogue
Pour finir, on peut s’interroger sur la valeur de la constante ![]() définie comme étant la borne inférieure de l’ensemble des réels
définie comme étant la borne inférieure de l’ensemble des réels ![]() pour lesquels :
pour lesquels :
![]()
Nous avons établi ci-dessus que :
![]()
Par ailleurs, un théorème de Hurwitz stipule que, si ![]() alors il existe une infinité de couples
alors il existe une infinité de couples ![]() d’entiers premiers entre eux tels que :
d’entiers premiers entre eux tels que :
![]()
En outre, si ![]() n’est pas de la forme
n’est pas de la forme ![]() avec
avec ![]() ,
, ![]() et
et ![]() , on peut montrer que :
, on peut montrer que :
![]()
On obtient ainsi l’encadrement suivant :
![Rendered by QuickLaTeX.com \[\boxed{2\sqrt{2}\leqslant\gamma\left(\sqrt{2}\right)\leqslant\sqrt{2}+\frac{\sqrt{10}}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1213d66896646d666bf31f1af06cd25c_l3.png)
Autre solution (sans recourir à l’inégalité des accroissements finis)
Soient ![]() . Comme
. Comme ![]() est irrationnel, l’entier
est irrationnel, l’entier ![]() n’est pas nul. Par conséquent :
n’est pas nul. Par conséquent :
![]()
![]()
d’où :
![Rendered by QuickLaTeX.com \[\left|\frac{p}{q}-\sqrt{2}\right|\geqslant\frac{1}{q^{2}\,\left(\frac{p}{q}+\sqrt{2}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c4e70e5d273cf98a143553522d0ac6a7_l3.png)
Si l’on suppose ![]() , alors :
, alors :
![Rendered by QuickLaTeX.com \[\left|\frac{p}{q}-\sqrt{2}\right|\geqslant\frac{1}{q^{2}\,\left(2+\sqrt{2}\right)}>\frac{1}{4\,q^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-63c6dc11c34b88853bc31c1f01a3666b_l3.png)
Et si ![]() , alors :
, alors :
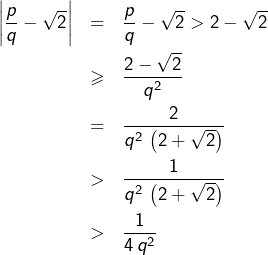
Pour consulter l’énoncé, c’est ici

