Solution pour le challenge n° 41

Considérons une bijection continue et (strictement) croissante :

$\varphi :[0,1 [\to[ 1,+\infty [$

Nécessairement $\varphi(0)=1$ (en effet, si l’on avait $\varphi(0)>1$ , alors aucun élément de $[1,\varphi(0)[$ ne posséderait d’antécédent, en raison de la croissance de $\varphi$ . Et ceci contredirait la surjectivité de $\varphi$ ).

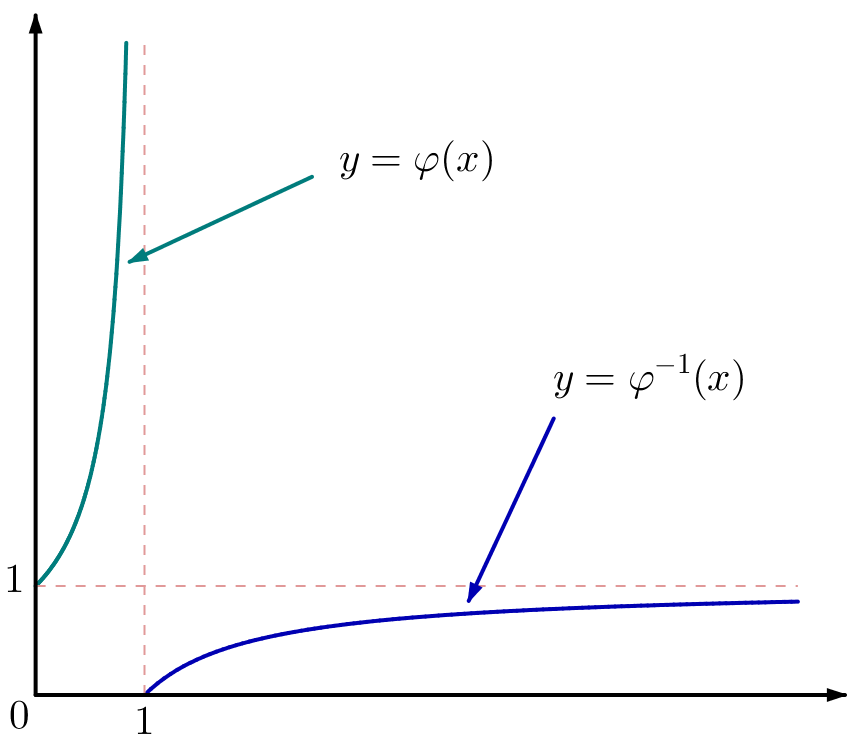
Pour fixer les idées, on peut choisir par exemple :

$\varphi:[0,1 [\to[1,+\infty[,\;x\mapsto\frac1{1-x}$

(ce qui correspond au graphe ci-dessous) mais ce n’est pas une obligation.

Définissons maintenant :

$\boxed{f:[0,+\infty[\to[0,+\infty[,x\mapsto\left\{\begin{matrix}\varphi(x) &\text{si }0\leqslant x<1\\\varphi^{-1}(x) &\text{si }x\geqslant1\end{matrix}\right.}$

On constate que, pour tout $x\in[0,1[$ :

$f(f(x))=\varphi^{-1}(\varphi(x))=x$

et, pour tout $x\in[1,+\infty[$ :

$f(f(x))=\varphi(\varphi^{-1}(x))=x$

Ainsi $f$ est une involution (ce qui signifie simplement que $f\circ f=id_{[0,+\infty[}$ ) et ceci montre en particulier son caractère bijectif.

En outre, $f$ est continue en 0 et $f^{-1}$ (c’est-à-dire $f$ ) est discontinue en $1=f(0)$ .

Ceci est à comparer à la “version continue” du théorème de la bijection (il existe une version dérivable, une version $\mathcal{C}^k$ …), dont l’énoncé est rappelé ci-dessous :

Théorème

Soient $I,J$ deux intervalles (de longueurs non nulles) de $\mathbb{R}$ .

Si $u:I\to J$ est une bijection continue, alors sa réciproque $u^{-1}$ est continue.

L’exemple construit plus haut montre que l’énoncé modifié en fixant $a\in I$ et en remplaçant :

dans l’hypothèse, la continuité globale (ie : en tout point de 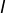$I$ ) de $u$ par sa continuité en $a$
la conclusion par la continuité de 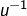$u^{-1}$ en $u(a)$

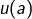
est FAUX.

Pour consulter l’énoncé, c’est ici

Partager cet article

Théorème

Laisser un commentaire Annuler la réponse