Solution pour le challenge n° 38

Solution pour le challenge 38

On sait bien qu’il existe des surjections de $\left[0,1\right]$ dans $\mathbb{R}.$

En voici un exemple parmi tant d’autres :

$s(x)=\left\{ \begin{array}{cc}{\displaystyle \frac{2x-1}{x\left(1-x\right)}} & \text{si }0<x<1\\\\0 & \text{si }x\in\left\{0,1\right\}\end{array}\right.$

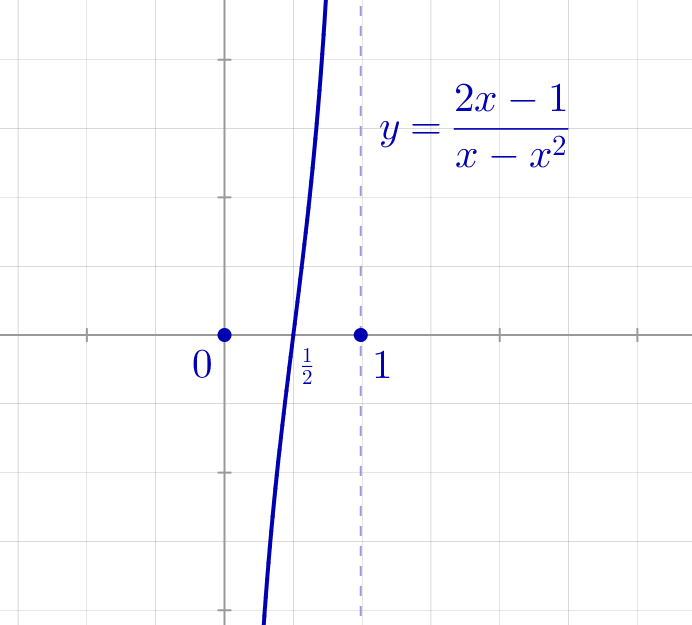
Si l’on peut construire une application $f:\mathbb{R}\rightarrow\mathbb{R}$ telle que l’image directe de tout intervalle non-trivial soit $\left[0,1\right]$ , il suffira ensuite de considérer $s\circ f$ pour répondre affirmativement à ce challenge.

Pour cela, étant donné $x\in\mathbb{R}$ , écrivons son développement décimal propre :

$x=\left\lfloor x\right\rfloor +\sum_{k=1}^{\infty}a_{k}\left(x\right)\thinspace10^{-k}$

avec $a_{k}\left(x\right)\in\llbracket0,9\rrbracket$ pour tout $k\in\mathbb{N}^{\star}$ , et les $a_{k}\left(x\right)$ qui ne sont pas tous égaux à 9 à partir d’un certain rang.

Définissons alors $f\left(x\right)$ comme étant la fréquence du chiffre 1 dans la suite $\left(a_{k}\left(x\right)\right)_{k\geqslant1}$ , à savoir :

$\boxed{f(x)=\lim_{n\rightarrow\infty}\frac{1}{n}\,\text{card}\left(E_n(x)\right)}$

où l’on a posé :

$E_n(x)=\left\{k\in\llbracket 1,n\rrbracket;\thinspace a_{k}\left(x\right)=1\right\}$

… si toutefois cette limite existe !

Et si elle n’existe pas, posons $\boxed{f\left(x\right)=0}$ .

Il s’agit de prouver que, si $I=\left[u,v\right]$ avec $u<v$ , alors $f\left\langle I\right\rangle =\left[0,1\right]$ .

Etant donné $\alpha\in\left[0,1\right]$ , posons pour tout $n\geqslant1$ :

$b_{n}=\left\lfloor n\alpha\right\rfloor -\left\lfloor \left(n-1\right)\alpha\right\rfloor$

Alors $b_n\geqslant0$ et $b_{n}<n\alpha-\left(\left(n-1\right)\alpha-1\right)=\alpha+1\leqslant2$ . Donc : $b_{n}\in\left\{ 0,1\right\}$ .

Considérons le réel :

$y=\sum_{n=1}^{\infty}b_{n}\thinspace10^{-n}\in\left[0,\frac{1}{9}\right]\subset\left[0,1\right[$

Il est clair (sommation télescopique) que :

$\frac{1}{n}\,\text{card}\left(E_n(x)\right) =\frac{1}{n}\sum_{k=1}^{n}b_{k}=\frac{\left\lfloor n\alpha\right\rfloor }{n}$

d’où, en passant à la limite :

$f\left(y\right)=\alpha$

Pour finir, en choisissant $x\in I$ dont le développement décimal propre coïncide à partir d’un certain rang avec celui de $y$ , on constate que $f\left(x\right)=\alpha$ . On a bien montré que $f\left\langle I\right\rangle =\left[0,1\right]$ .

J’aurais bien aimé vous dessiner le graphe de $s\circ f$ … mais je crains que ce ne soit pas dans mes cordes

Le graphe de $f$ est une sorte « ruban » horizontal infini, avec des ordonnées comprises entre 0 et 1, mais attention : un ruban « poreux » !! Car il faut essayer d’imaginer que pour toute abscisse $x,$ le segment vertical joignant les points $\left(x,0\right)$ et $\left(x,1\right)$ ne contient qu’un seul point du graphe …

Pour le graphe de $s\circ f,$ c’est la même idée mais cette fois les ordonnées s’étendent de $-\infty$ à $+\infty$ .

On doit pouvoir montrer que le graphe de $s\circ f$ est une partie dense de $\mathbb{R}^{2}$ . Des candidats ?

Pour consulter l’énoncé, c’est ici

Partager cet article

Laisser un commentaire Annuler la réponse