Solution pour le challenge 29
La clef de cette histoire est l’identité :![]()
qui est valable pour tout ![]() .
.
On raisonne alors par récurrence, en observant pour commencer que :
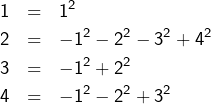
Ensuite, si l’on dispose, pour un certain ![]() , d’une décomposition du type :
, d’une décomposition du type :
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}n+4&=&\left[\sum_{i=1}^{r}\epsilon_{i}i^{2}\right]\\& &+\left(r+1\right)^{2}\\& &-\left(r+2\right)^{2}\\& &-\left(r+3\right)^{2}\\&& +\left(r+4\right)^{2}\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-aff9dd27883adc7992c90be286685a13_l3.png)
Pour consulter l’énoncé, c’est ici

