Solution pour le challenge 27
On va raisonner par analyse / synthèse, en tâchant de borner l’ensemble des solutions.
Supposons que ![]() soit un couple solution.
soit un couple solution.
Alors ![]() et donc, vu que :
et donc, vu que :
![]()
![]()
A fortiori ![]() c’est-à-dire
c’est-à-dire ![]() et donc nécessairement :
et donc nécessairement :
![]()
Réciproquement, il faut maintenant passer en revue ces différentes possibilités, en reportant à chaque fois dans l’équation initiale :
- Si
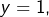 alors :
alors :![Rendered by QuickLaTeX.com \[x^{3}-x-62=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ebd1b4cf913b8851a52893a9c75faacc_l3.png)
- Si
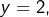 alors :
alors :![Rendered by QuickLaTeX.com \[x^{3}-2x-69=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-af0238d73d698406ec8ce9bdb5ded296_l3.png)
- Si
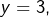 alors :
alors :![Rendered by QuickLaTeX.com \[x^{3}-3x-88=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d3b9e607f9ba8fc91463c69de2941f29_l3.png)
- Si
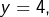 alors :
alors :![Rendered by QuickLaTeX.com \[x^{3}-4x-125=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3827ff6cfe94c83c9f09dffa6ee733ff_l3.png)
- Si
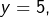 alors :
alors :![Rendered by QuickLaTeX.com \[x^{3}-5x-186=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-53c12c9219adb03d571e7e9136037576_l3.png)
En utilisant le test des racines rationnelles (voir par exemple cet article), on vérifie que seule la dernière équation (associée à ![]() ) admet une solution dans
) admet une solution dans ![]() et qu’il s’agit de
et qu’il s’agit de ![]()
Finalement, l’ensemble des solutions est réduit au singleton ![]()
Pour consulter l’énoncé c’est ici

