Solution pour le challenge n° 26

Solution pour le challenge 26

Partons de la relation :

$F_{n+2}=F_{n+1}+F_{n}\qquad\left(\heartsuit\right)$

En élevant chaque membre au carré puis en isolant le double-produit, on obtient :

$F_{n+2}^{2}-F_{n+1}^{2}-F_{n}^{2}=2F_{n+1}F_{n}\qquad\left(\star\right)$

En remplaçant $n$ par $n+1,$ ceci devient :

$F_{n+3}^{2}-F_{n+2}^{2}-F_{n+1}^{2}=2F_{n+2}F_{n+1}$

Et donc, d’après $\left(\heartsuit\right)$ :

$F_{n+3}^{2}-F_{n+2}^{2}-F_{n+1}^{2}=2\left(F_{n+1}+F_{n}\right)F_{n+1}$

c’est-à-dire :

$F_{n+3}^{2}-F_{n+2}^{2}-3F_{n+1}^{2}=2F_{n+1}F_{n}$

On reconnaît le membre de droite de $\left(\star\right)$ et par conséquent :

$F_{n+3}^{2}-F_{n+2}^{2}-3F_{n+1}^{2}=F_{n+2}^{2}-F_{n+1}^{2}-F_{n}^{2}$

Finalement, en notant $C_{n}$ pour $F_{n}^{2},$ on a prouvé que :

$\boxed{\forall n\in\mathbb{N},\thinspace C_{n+3}=2C_{n+2}+2C_{n+1}-C_{n}}\qquad\left(\diamondsuit\right)$

Compte tenu des « conditions initiales » :

$C_{0}=0,\qquad C_{1}=1,\qquad C_{2}=1$

et de la relation $\left(\diamondsuit\right)$ il est facile d’obtenir les valeurs des termes suivants :

$C_{3}=4,\qquad C_{4}=9,\qquad C_{5}=25$

$C_{6}=64,\qquad C_{7}=169,\qquad C_{8}=441,\qquad\text{etc ...}$

Passons au deuxième point.

On sait (formule de Jacques Binet) que :

$\boxed{\forall n\in\mathbb{N},\quad F_{n}=\frac{1}{\sqrt{5}}\left(\alpha^{n}-\beta^{n}\right)}$

où l’on a posé :

$\alpha=\frac{1+\sqrt{5}}{2}\qquad\text{et}\qquad\beta=\frac{1-\sqrt{5}}{2}$

Comme $\alpha>1$ tandis que $\left|\beta\right|<1,$ il en résulte notamment que :

$F_{n}\sim\frac{\alpha^{n}}{\sqrt{5}}$

et donc que :

$C_{n}\sim\frac{\alpha^{2n}}{5}$

Ceci permet de voir que le rayon de convergence de la série entière $\sum_{n\geqslant0}C_{n}x^{n}$ est :

$\boxed{R=\lim_{n\rightarrow\infty}\frac{C_{n}}{C_{n+1}}=\frac{1}{\alpha^{2}}=\frac{3-\sqrt{5}}{2}\simeq0,382}$

Notons $f$ sa somme :

$\forall x\in\left]-R,R\right[,\:f\left(x\right)=\sum_{n=0}^{\infty}C_{n}x^{n}$

Pour tout $x\in\left]-R,R\right[,$ la sommation des égalités :

$C_{n+3}x^{n+3}-2xC_{n+2}x^{n+2}-2x^{2}C_{n+1}x^{n+1}+x^{3}C_{n}x^{n}=0$

(qui sont valables pour tout $n\in\mathbb{N}$ ) conduit à :

$\left(f\left(x\right)-x-x^{2}\right)-2x\left(f\left(x\right)-x\right)-2x^{2}f\left(x\right)+x^{3}f\left(x\right)=0$

c’est-à-dire

$\left(x^{3}-2x^{2}-2x+1\right)f\left(x\right)=x-x^{2}$

Le polynôme $Q$ défini par $Q\left(x\right)=x^{3}-2x^{2}-2x+1$ se factorise comme suit (voir éventuellement cet article pour réviser les techniques de base de factorisation) :

$\begin{eqnarray*}Q\left(x\right)&=&\left(x+1\right)\left(x^{2}-3x+1\right)\\&=&\left(x+1\right)\left(x-\frac{3-\sqrt{5}}{2}\right)\left(x-\frac{3+\sqrt{5}}{2}\right)\end{eqnarray*}$

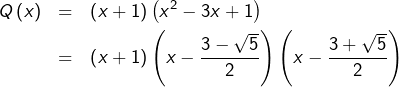
Parmi les trois racines de $Q$ , celle de plus petite valeur absolue est $\frac{3-\sqrt{5}}{2}=R.$

Ainsi $Q\left(x\right)$ ne s’annule pas pour $x\in\left]-R,R\right[$ et l’on obtient finalement :

$\boxed{\forall x\in\left]-R,R\right[,\quad\sum_{n=0}^{\infty}C_{n}x^{n}=\frac{x-x^{2}}{x^{3}-2x^{2}-2x+1}}\qquad\left(\heartsuit\right)$

C’est ce qu’on appelle la série génératrice de la suite $\left(C_{n}\right)_{n\in\mathbb{N}}$ .

Avec un logiciel de calcul formel, il est facile d’obtenir les premiers termes du développement de la fraction rationnelle qui apparaît au membre de droite de $\left(\heartsuit\right)$ .

Voici typiquement ce qu’on obtient (ici dans la syntaxe de Maple) :

taylor ((x-x^2)/(x^3-2*x^2-2*x+1), x=0, 9);

x + x^2 + 4 x^3 + 9 x^4 + 25 x^5 + 64 x^6 + 169 x^7 + 441 x^8 + O(x^9)

Les coefficients des monômes $1,$ $x,$ $x^{2},$ etc … $x^{8}$ sont bien les carrés des 9 premiers nombres de Fibonacci.

Pour consulter l’énoncé, c’est ici

Partager cet article

Laisser un commentaire Annuler la réponse