Solution pour le challenge 20
Nous allons raisonner par l’absurde. Supposons l’existence d’un nombre rationnel ![]() vérifiant :
vérifiant :
![]()
et posons :
![]()
D’après la formule de Moivre :
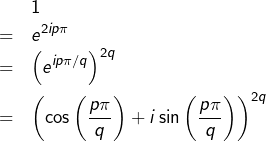
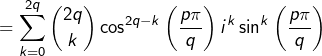
Donc, en passant aux parties réelles :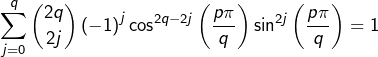
et, compte tenu de l’hypothèse ![]() :
: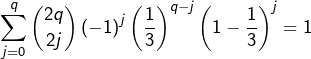
Après simplification, il reste :
![Rendered by QuickLaTeX.com \[\sum_{j=0}^{q}\binom{2q}{2j}\left(-1\right)^{j}2^{j}=3^{q}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-81b2d1a43ae796dd8b804d245979b0e4_l3.png)
Ceci entraîne en particulier que :
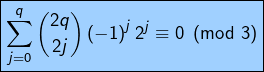
Pourtant, vu que ![]() il vient pour tout
il vient pour tout ![]() :
:
![]()
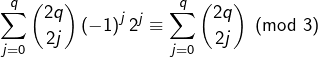
Or :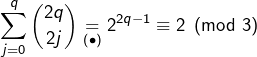
ce qui est contradictoire.
Remarque
Dans l’égalité ![]() on s’est servi du fait que pour tout entier
on s’est servi du fait que pour tout entier ![]() :
:
![Rendered by QuickLaTeX.com \[\boxed{\sum_{j=0}^{\left\lfloor N/2\right\rfloor }\binom{N}{2j}=2^{N-1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-06bbc1a1dfb1315bd593f3403d11494b_l3.png)
Ce résultat classique peut être établi en observant que, si l’on note :
![Rendered by QuickLaTeX.com \[A=\sum_{j=0}^{\left\lfloor N/2\right\rfloor }\binom{N}{2j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9f48b00ade603583bc7e7716ce84d69d_l3.png)
![Rendered by QuickLaTeX.com \[B=\sum_{j=0}^{\left\lfloor (N-1)/2\right\rfloor }\binom{N}{2j+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bcab0fc607b2bc9cf8a2a5d4b3f909f1_l3.png)
![Rendered by QuickLaTeX.com \[A+B=\sum_{k=0}^{N}\binom{N}{k}=2^{N}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7014d99d5c9213efbefdfa1a9c77a299_l3.png)
Pour consulter l’énoncé, c’est ici

