Solution pour le challenge n° 19

Solution pour le challenge 19

Posons, pour tout $n\geqslant2,$

$u_{n}=\frac{H_{n}}{\ln\left(n\right)}$

et cherchons le signe de $u_{n+1}-u_{n}.$

Dans ce qui suit, on notera $x\,\sharp\,y$ pour indiquer que $x$ et $y$ sont de même signe.

En multipliant par $\displaystyle{\frac{\ln\left(n+1\right)}{H_{n}}}$ qui est strictement positif, il vient :

$\begin{eqnarray*}& &u_{n+1}-u_{n}\\& = & \frac{H_{n+1}}{\ln\left(n+1\right)}-\frac{H_{n}}{\ln\left(n\right)}\\& \sharp\ & \frac{H_{n+1}}{H_{n}}-\frac{\ln\left(n+1\right)}{\ln\left(n\right)}\\& \underset{\textrm{déf}}{=} & d_{n}\end{eqnarray*}$

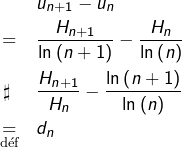
D’après les relations :

$\frac{H_{n+1}}{H_{n}}=1+\frac{1}{\left(n+1\right)H_{n}}$

$\begin{eqnarray*}& &\frac{\ln\left(n+1\right)}{\ln\left(n\right)}\\&=&1+\frac{1}{\ln\left(n\right)}\ln\left(1+\frac{1}{n}\right)\end{eqnarray*}$

il vient :

$d_{n}\enspace\sharp\enspace\frac{1}{H_{n}}-\frac{n+1}{\ln\left(n\right)}\ln\left(1+\frac{1}{n}\right)$

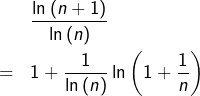
Or, on sait que :

$\forall t>-1,\ln\left(1+t\right)\leqslant t\qquad\left(\spadesuit\right)$

donc (en prenant $t=-\frac{1}{n+1})$ :

$\ln\left(1-\frac{1}{n+1}\right)\leqslant-\frac{1}{n+1}$

c’est-à-dire :

$\ln\left(1+\frac{1}{n}\right)\geqslant\frac{1}{n+1}$

Ainsi, d’après la minoration classique $H_{n}\geqslant\ln\left(n+1\right)>\ln\left(n\right)$ (voir détail ci-dessous) :

$\begin{eqnarray*}& &\frac{1}{H_{n}}-\frac{n+1}{\ln\left(n\right)}\ln\left(1+\frac{1}{n}\right)\\&\leqslant&\frac{1}{H_{n}}-\frac{1}{\ln\left(n\right)}<0\end{eqnarray*}$

et donc $d_{n}<0,$ ce qui prouve la décroissance de la suite étudiée.

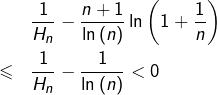
Détail (cliquer pour déplier / replier)

Afin de prouver que $\forall n\in\mathbb{N}^\star,\,H_n\geqslant\ln(n+1)$ , il suffit de voir que pour tout $k\in\llbracket1,n\rrbracket$ :
$\ln(k+1)-\ln(k)=\ln\left(1+\frac 1k\right)$
et (avec $\spadesuit$ ) que :
$\ln\left(1+\frac 1k\right)\leqslant\frac 1k$
puis d’effectuer, membre à membre, la sommation (télescopique) de ces inégalités.

Pour consulter l’énoncé, c’est ici

Partager cet article

Laisser un commentaire Annuler la réponse