Solution pour le challenge n° 17

Solution pour le challenge 17

Il est crucial de faire apparaître les écarts $\vert u_{k+1}-u_{k}\vert$ , car ils sont tous majorés par 1 et c’est la seule hypothèse que nous ayons.

Pour cela, on effectue une transformation d’Abel, c’est-à-dire en quelque sorte une « intégration par parties discrète » :

$\begin{eqnarray*}& &\sum_{k=1}^{n+1}u_{k}\\& = & \sum_{k=1}^{n+1}\left[k-\left(k-1\right)\right]u_{k}\\& = & \sum_{k=1}^{n+1}ku_{k}-\sum_{k=0}^{n}ku_{k+1}\end{eqnarray*}$

et donc (le terme d’indice 0 dans la dernière somme étant nul) :

$\begin{eqnarray*}& &\left(n+1\right)u_{n+1}-\sum_{k=1}^{n+1}u_{k}\\&=&\sum_{k=1}^{n}k\left(u_{k+1}-u_{k}\right)\end{eqnarray*}$

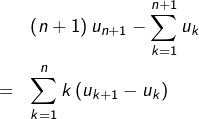
On divise alors chaque membre par $n\left(n+1\right),$ ce qui donne :

$\frac{u_{n+1}}{n}-\left(\frac{1}{n}-\frac{1}{n+1}\right)\sum_{k=1}^{n+1}u_{k}$

$=\frac{1}{n\left(n+1\right)}\sum_{k=1}^{n}k\left(u_{k+1}-u_{k}\right)$

c’est-à-dire :

$\displaystyle{\boxed{X_{n+1}-X_{n}=\frac{1}{n\left(n+1\right)}\sum_{k=1}^{n}k\left(u_{k+1}-u_{k}\right)}}$

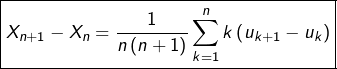
On applique maintenant l’inégalité triangulaire :

$\begin{eqnarray*}& &\left|X_{n+1}-X_{n}\right|\\& \leqslant & \frac{1}{n\left(n+1\right)}\sum_{k=1}^{n}k\left|u_{k+1}-u_{k}\right|\\& \leqslant & \frac{1}{n\left(n+1\right)}\sum_{k=1}^{n}k\end{eqnarray*}$

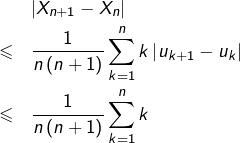
et comme 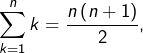$\sum_{k=1}^{n}k=\frac{n\left(n+1\right)}{2},$ on conclut que :

$\boxed{\left|X_{n+1}-X_{n}\right|\leqslant\frac{1}{2}}$

En outre, cette majoration est optimale puisque si $u_{n}=n$ pour tout $n\geqslant1,$ alors l’hypothèse est bien vérifiée et, pour tout $n\geqslant1$ :

$X_{n}=\frac{1}{n}\sum_{k=1}^{n}k=\frac{n+1}{2}$

d’où :
$\displaystyle{X_{n+1}-X_{n}=\frac{n+2}{2}-\frac{n+1}{2}=\frac{1}{2}}$

Pour consulter l’énoncé, c’est ici

Partager cet article

Laisser un commentaire Annuler la réponse